[수업출처] 숙명여자대학교 소프트웨어학부 유석종 교수님 수업 '자료구조'
1. Data Structures
- 문제 해결을 위한 대량의 데이터를 효율적으로 처리하고 조직하는 방법 또는 구조
- Linear DS: list, stack, queue, deque
- Non-Linear DS: tree, graph
- Advanced DS: BST, Weight networks
- Searching and Sorting algorithms
2. Algorithm
- 특정 작업을 수행하기 위한 명령어들의 유한한 집합
- 조건
- Input: 명시적 입력이 필요하지 않다.
- Output: 적어도 하나의 출력값이 있어야 한다.
- Definiteness: 구체적이고 모호하지 않은 명령어들의 집합이어야 한다.
- Finiteness: 유한한 단계를 거친 후 끝나야 한다.
- Effectiveness: 쓸모 있어야하고, 효율적이어야 한다.
- 표현 방법
- Pseudo code, Flow chart
- 자연어, 프로그래밍 언어
3. System Life Cycle
- Requirement 요구사항 명세
- 프로젝트의 목적을 정의하는 일련의 설계 명세서
- 사용자, 플랫폼, 함수, 인터페이스 등
- Analysis 분석
- 큰 프로젝트를 작은 모듈들로 나누는 과정
- Divide and conquer 전략
- Top-down approach
- 주 목적에서 구성요소로 가는 계층적 접근
- program -> subroutines -> instructions
- Bottom-up approach
- 구성요소가 모여 전체 시스템이 되는 방법
- Design 설계
- 각 모듈에 대한 객체와 함수 정의
- Implementation 구현
- 객체 및 알고리즘 코드 구현
- Verification 검증
- 알고리즘의 정확성 증명
- program test: black-box test, white-box test
4. Fibonacci Numbers
# fb는 리스트
def fibo(fb):
a = 0
b = 1
fb.append(a)
fb.append(b)
while True:
a, b = b, a+b
if b < n: break
fb.append(b)피보나치 수열을 구하는 함수이다.
리스트에 우선 0과 1을 넣고, b가 n이 되기 전까지 a = b, b = a+b로 대입하여 b, 즉 a+b를 리스트에 추가한다.
n = 100000
fb = []
fibo(fb)
print(fb)
print("# of fibos", len(fb))
5. Prime Numbers
- 소수: 1보다 큰 자연수 중 1과 자기자신 이외의 수로 나누어 떨어지지 않는 수
def find_prime(num):
for i in range(2, num+1):
prime = 1
for j in range(2, i):
if i % j == 0:
prime = 0
break
if prime: prime_list.append(i)2부터 num까지의 수를 각각 i로 둘 때, i를 2부터 i까지의 수로 나누어 본다.
이 때, 나누어 떨어지면 소수가 아니기 때문에 prime = 0으로 둔다.
i까지 전부 나눈 후 prime이 여전히 1이면 소수이기 때문에 prime_list에 추가한다.
이 과정을 num까지 반복한다.
prime_list = []
max_num = 1000
find_prime(max_num)
for i in range(2, max_num):
if i in prime_list: print('%3d' %i, end = '')
else: print('_', end = '')
if i % 50 == 0: print()
print()
print('# of prime numbers = ', len(prime_list))
6. Data Types
- 객체와 해당 객체에 작용하는 명령어들의 집합
- 내장 자료형
- Basic type: char, int, float
- Collection type: string, list, tuple, set, dictionary
- 추상 자료형
- 객체의 자료형
7. Abstract Data Type (ADT) 추상 자료형
- 객체의 속성(attributes, properties, member variables)과 행동(methods, operations, member funtions)을 추상화하는 자료형
- 사용자가 필요에 의해 자료형을 직접 정의하는 것
- 객체지향 프로그래밍에서는 공통적인 행위를 하는 Class를 정의한다.
- ex) bank account, student, fraction
8. Fraction 분수
- 분자와 분모로 이루어져 있다.
- 기본적으로 분수는 내장되어있지 않기 때문에 객체로 정의해주어야 한다.
- 약분까지 해야 함 -> gcd(x, y)
class Fraction:
def __init__(self, up, down):
self.num = up
self.den = down
def __str__(self):
return str(self.num) + '/' + str(self.den)
def __add__(self, other):
new num = self.num * other.den + self.den * other.num
new_den = self.den * other.den
common = self.gcd(new_num, new_den)
return Fraction(new_num//common, new_den//common
def multiply(self, other):
new num = self.num * other.num
new_den = self.den * other.den
common = self.gcd(new_num, new_den)
return Fraction(new_num//common, new_den//common)
def gcd(self, a, b):
while a % b != 0:
a, b = b, a % b
return bdef __init__(self, up, down)은 Fraction 클래스를 호출했을 때 두번째 매개변수 up을 self.num에, 세번째 매개변수 down을 self.den에 대입하는 메서드이다. 이때 self.num은 분자, self.den은 분모이다.
def __str__(self)는 print(Fraction(up, down)을 실행했을 때 호출되는 메서드이다. 분수형태로 출력해준다.
def __add__(self, other)는 덧셈 메서드이다. + 로 두 변수를 연결했을 때 자동으로 호출된다.
분자는 self의 분자 x other의 분모 + self의 분모 x other의 분자이고,
분모는 self의 분모 x other의 분모이다.
common은 덧셈 결과의 분자와 분모의 최대공약수로, 이후에 나올 gcd 메서드를 통해 구할 수 있다.
최종적으로 덧셈 결과의 분자와 분모를 최대공약수로 약분해서 결과를 도출한다.
def multiply(self, other)는 곱셈 메서드이다.
분자는 self의 분자와 other의 분자를 곱한 값이고,
분모는 self의 분모와 other의 분모를 곱한 값이다.
마찬가지로 gcd 메서드로 최대공약수를 구한 후 곱셈 결과를 약분해서 도출한다.
def gcd(self, a, b)는 분자와 분모의 최대공약수를 구하는 메서드이다.
gcd(a, b) = gcd(b, a%b) 공식을 이용하였다.
num1 = Fraction(1, 4)
num2 = Fraction(1, 2)
num3 = num1 + num2
print(num1, '+', num2, '=', num3)
num1 = Fraction(3, 4)
num2 = Fraction(2, 9)
num3 = num1.multiply(num2)
print(num1, '*' num2, '=', num3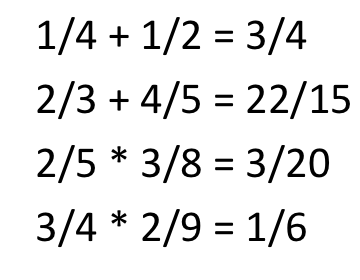
9. Performance Analysis
- 이상적 기준 → 추상적
- 고객의 요구사항을 만족하는지?
- 잘 작동하는지?
- 효율적으로 구현했는지?
- 현실적 기준 → 객관적 수치 도출
- 공간복잡도: 실행할 때 메모리 공간을 얼마나 사용하는지
- 시간복잡도: 연산 시간이 얼마나 소요되는지
10. 공간복잡도 Space Complexity
- Fixed space requirements(Sc) : 명령어, 단순 변수, 고정크기의 구조체 변수, 상수 등으로 컴파일 전에 알 수 있음
- Variable space requirements(Sv): 배열 함수 전달, 재귀호출 등으로 실행 중에 결정됨. Sv를 구해야 함
- S = Sc + Sv
def abc(a, b, c):
return a + b * c + (a + b - c) / (a + b) + 4.00- input: 3개의 단순 변수
- output: 1개의 단순 변수
- 배열 전달, 재귀 X → 가변 요구공간 = 0
- 고정 요구공간은 있지만 관심있는 부분이 아님
def iSum(num):
total = 0
for item in num:
total = total + num
return total- input: 배열(num)
- output: 단순 변수
- 공간복잡도는 배열 함수 전달 방법에 달려있음 (copy or 주소 전달)
- call by value
- 배열 요소들은 함수로 '복사'되어짐
- 배열 크기에 비례하여 추가적인 메모리 공간이 요구됨
- Sv = n
- ex) Pascal
- call by reference
- 배열의 시작 주소만 함수로 전달됨
- 추가적인 메모리 공간 요구되지 않음
- Sv = 0
- ex) C, Python
- 재귀호출
def rsum(sum):
if len(num):
return rsum(num[:-1]) + num[-1]
else:
return 0
print(rsum([1, 2, 3, 4, 5])- 함수가 호출될 때마다 현재 실행중인 문맥 모두 저장되어야 함
- variables, return address, n times funcion calls (rsum(n-1), ..., rsum(0))
- space complexity = n * (size(num) + return address)
11. 시간복잡도 Time complexity
- 알고리즘이 수행되는데 걸리는 시간
- T = compile time(Tc) + excution time(Te)
- 실행시간(Te)가 시간복잡도를 구할 때 사용되며, 실행 환경에 영향을 받음
→ 명령어 개수로 시간 측정, 명령어 별로 실행 시간 다른 것은 무시함
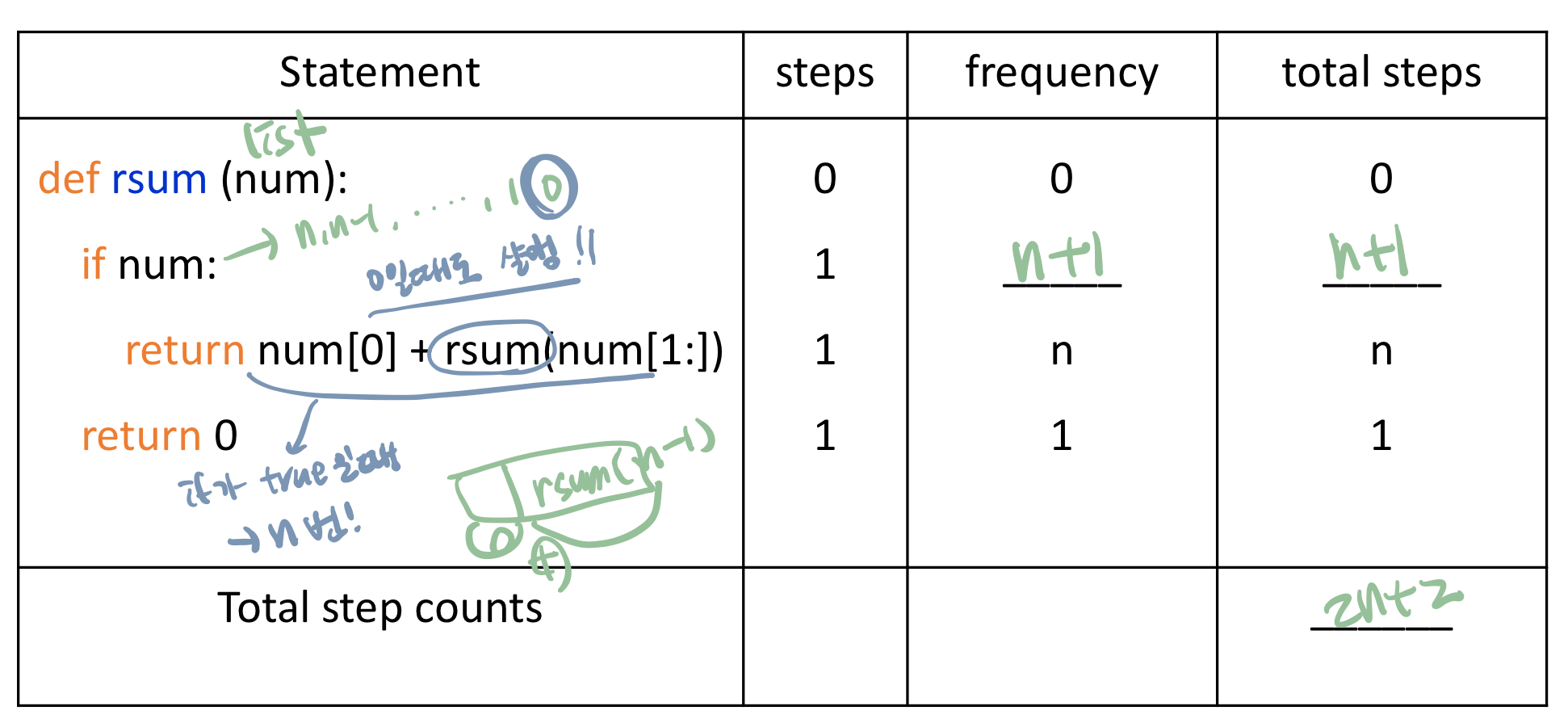
- Step count table
- steps: 한 라인에 명령어가 몇 개인지 (함수 헤더, 변수 선언은 무시함)
- frequency: 명령어가 몇 번 실행되는지 (for, while loops)
- total steps = steps * frequency per line


12. Big-O Notation
- n이 매우 큰 경우 시간복잡도 함수를 점근적으로 근사한 것
- n이 증가할 경우 알고리즘을 실행하는데 소요되는 시간
- 알고리즘 성능 평가를 위한 표준
- T(n) = n² + 2n → O(n²)
- f(n) ≤ c * g(n) for all n ≥ n0 를 만족하는 정수 n0와 c가 존재하면 Big-O notation 사용 가능
- c * g(n)은 f(n)의 상한선 → c * g(n)보다는 시간이 적게 걸림
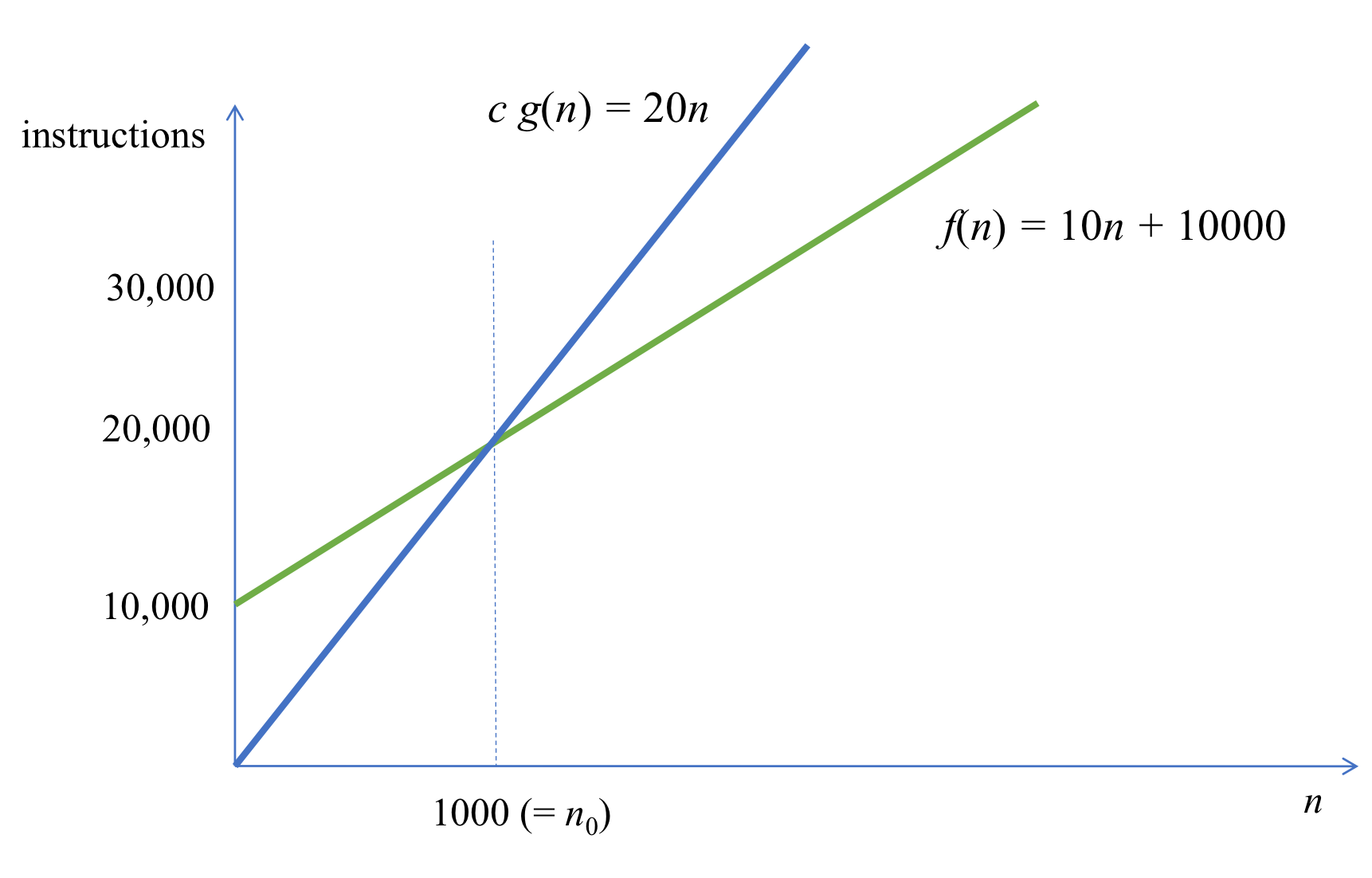
- ex) f(n) = 10n + 10,000 ∈ O(n)
- f(n) ≤ 20n (=c) for all n ≥ 1000 (=n0)
13. Big-Omega Notation
- f(n) ≥ c * g(n) for all n ≥ n0 를 만족하는 정수 n0와 c가 존재하면 Big-Omega notation 사용 가능
- c * g(n)은 f(n)의 하한선
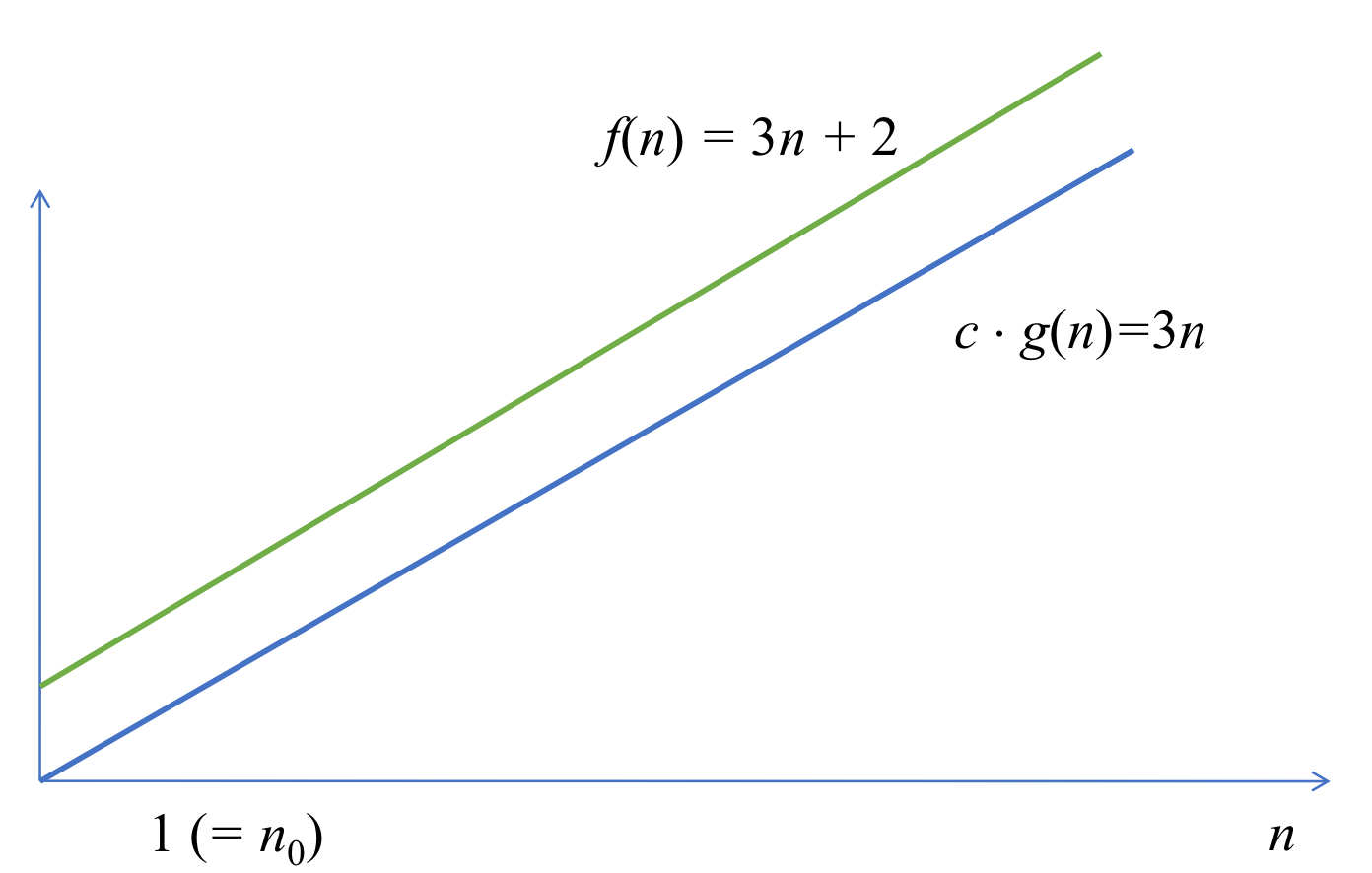
- ex) f(n) = 3n + 2 ∈ Ω(n)
- f(n) ≥ 3n for n ≥ 1
14. Big-Theta Notation
- f(n) ∈ Ω(n) 이고 f(n) ∈ O(n)을 만족하는 c1, c2, n0가 존재하면 f(n) ∈ θ(g(n()) 존재
- c1 * g(n) ≤ f(n) ≤ c2 * g(n) for all n ≥ n0
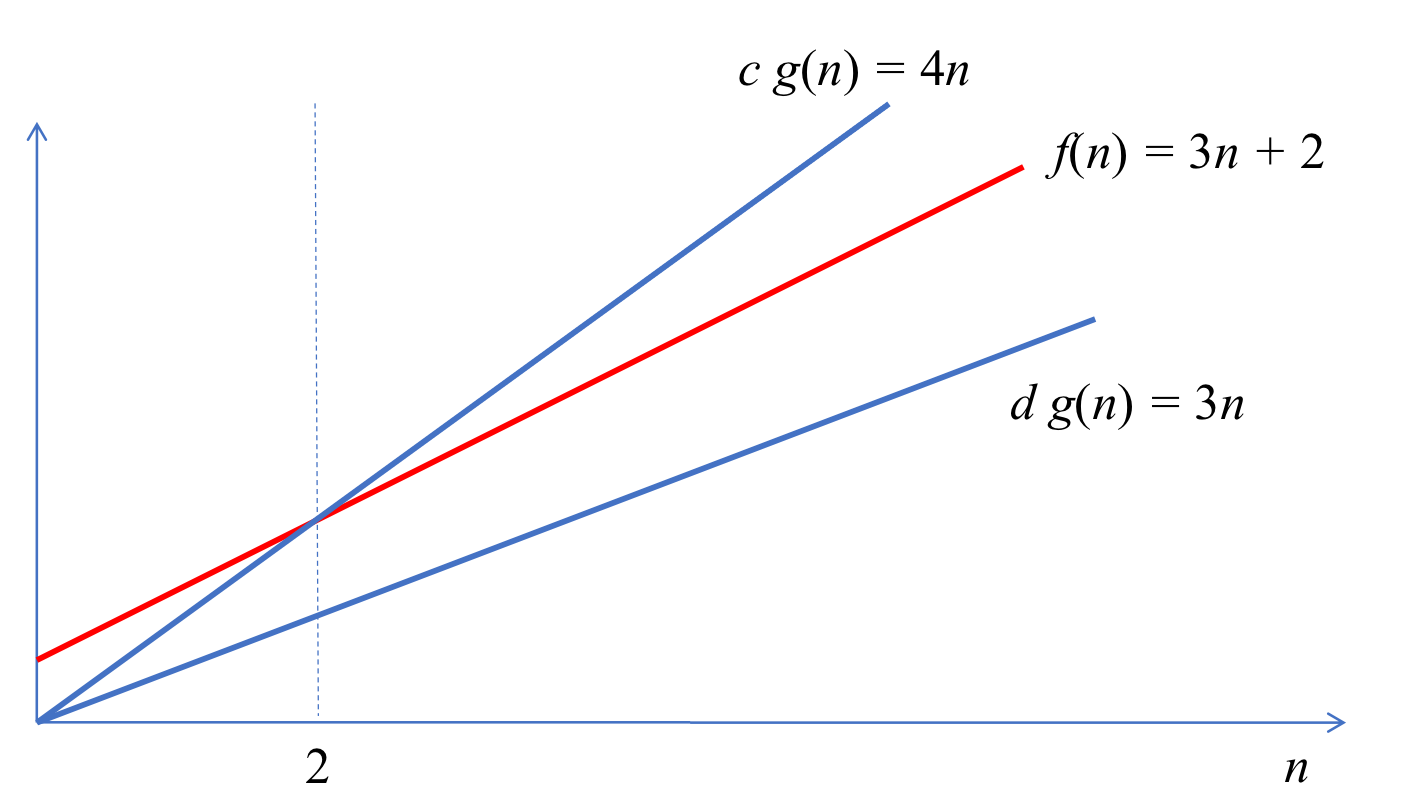
- ex) f(n) = 3n + 2 ∈ θ(n)
- 3n ≤ f(n) ≤ 4n for all n ≥ 2
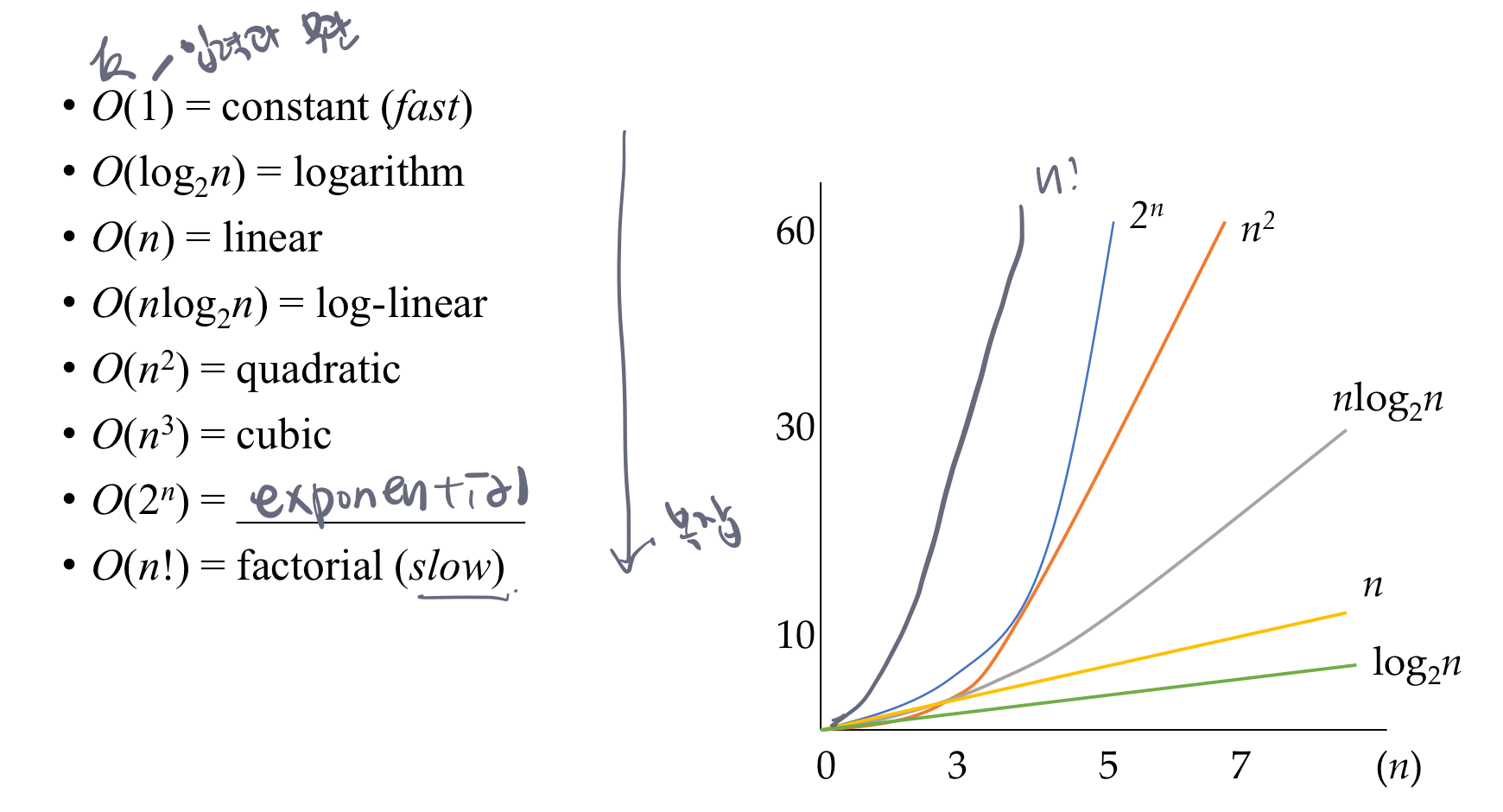
15. Time complexity class
'Software > Data Structures' 카테고리의 다른 글
| [Python] 2장 연습문제 (0) | 2022.04.16 |
|---|---|
| [Python] 2. Python Data Type (0) | 2022.04.16 |
| [자료구조] 탐색 (0) | 2021.04.20 |
| [자료구조] 연결 리스트 (0) | 2021.04.20 |
| [자료구조] 선형 자료구조 (0) | 2021.04.18 |