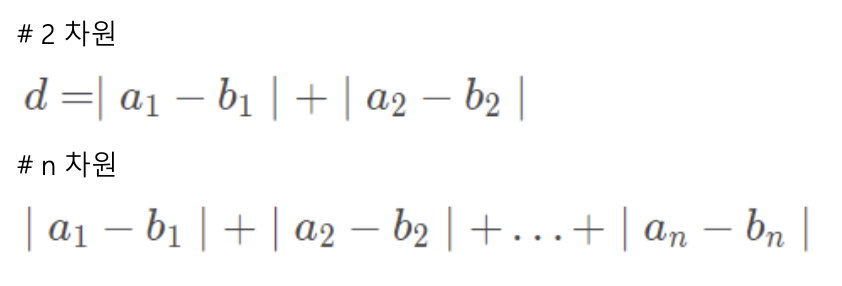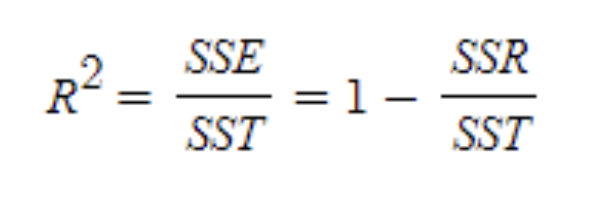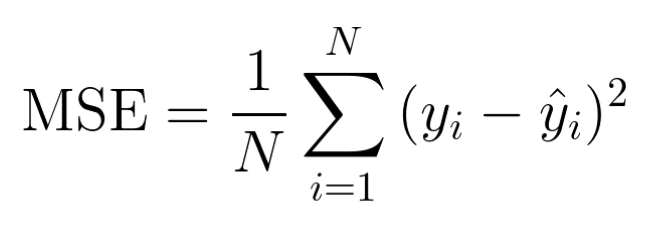1. 회귀 분석
- 독립변수 x에 대응하는 종속변수 y와 가장 유사한 값을 갖는 함수 f(x)를 찾는 과정
→ f(x)를 통해 미래 사건 예측
^y = f(x) ≈ y
- 회귀 분석을 통해 구한 함수 f(x)가 선형 함수일 때 f(x) = 회귀 직선
- 선형 회귀 분석
- 특성과 타겟 사이의 관계를 잘 나타내는 선형 회귀 모형을 찾고, 이들의 상관관계는 가중치/계수(m), 편향(b)에 저장됨
=> ^y = w * x + b
2. 비용 함수 = 손실 함수
- 선형 모델의 예측과 훈련 데이터 사이의 거리를 재는 함수
- 비용 함수의 결과값이 작을수록 선형 모델의 예측이 정확함
- 선형 회귀는 선형 모델이라는 가설을 세우는 방식이므로, 실제 데이터(훈련 데이터)와 선형 모델의 예측 사이에 차이 존재
- 실제 데이터와 선형 모델의 예측 사이의 차이를 평가하는 함수 → 비용 함수를 사용하여 정확도 계산
- MSE 가장 많이 사용 [실제값과 예측값의 차이인 오차들의 제곱의 평균]
3. 선형 회귀 구현
1) 선형 회귀 모델 구현
# 훈련 세트, 테스트 세트 생성
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight, random_stae = 42)
train_input = train_input.reshape(-1, 1)
test_input = test_input.reshape(-1, 1)
# 50cm 농어 평균 무게 예측
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_input, train_target)
print(lr.predict([50]))
# 1241.83860323
2) 회귀 확인
# 회귀 직선 ^y = W * x + b 구하기
print(lr.coef_, lr.intercept_)
# [39.01714496], -709.0186449535477
# => y = lr.coef_ * x + lr.intercept_
plt.plot([15, 50], [15*lr.coef_+lr.intercept_, 50*lr.coef_+lr.intercept_])
3) 훈련 세트 산점도 그리기
plt.plot([15, 50], [15*lr.coef_ + lr.intercept_, 50*lr.coef_ + lr.intercept_])
plt.scatter(train_input, train_target)
plt.scatter(50, 1241, 8, marker = '^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
- 회귀 직선이 어느 정도는 데이터를 잘 나타내고 있음
- 그러나, 훈련 세트와 테스트 세트 모두 결정 계수가 너무 낮음 → 과소 적합
+ 산점도에서 매우 작은 길이를 가진 농어의 경우 회귀 직선이 데이터를 설명하지 못함
4. 선형 회귀 모델의 최적화 → 경사 하강법
- 머신러닝, 딥러닝 알고리즘을 학습시킬 때 사용하는 방법
- 비용 함수의 기울기를 계속 낮은 쪽으로 이동시켜 극값(최적값)에 이를 때까지 반복하는 것
- 경사 하강법을 이용하여 비용 함수에서 기울기가 '0'일 때의 비용(오차)값을 구할 수 있음
- 비용 함수의 최소값을 구하면 이때 회귀 함수를 최적화 할 수 있게 됨
- 비용 함수에서 기울기가 '0'일 때 (비용 함수가 최솟값일 때) 모델의 기울기와 y절편을 구하여 회귀 함수 최적화

5. 경사 하강법 - learning rate(학습률)
- 선형 회귀에서 가중치(w)와 편향(b)을 경사 하강법에서 반복 학습시킬 때, 한 번 반복 학습시킬 때마다 포인트를 얼만큼씩 이동시킬 것인지 정하는 상수
- 학습률이 너무 작은 경우: local minimum에 빠질 수 있음
- 학습률이 너무 큰 경우: 수렴이 일어나지 않음
=> 적당한 learning rate를 찾는 것이 중요!
- 시작을 0.01로 시작해서 overshooting이 일어나면 값을 줄이고, 학습 속도가 매우 느리다면 값을 올리는 방향으로 진행
import numpy as np
import matplotlib.pyplot as plt
X = np.random.rand(100)
Y = 0.2 * X + 0.5 # 실제값 함수 가정
plt.figure()
plt.scatter(X, Y)
plt.show()
# 실제값, 예측값 산점도 그리는 함수
def plot_prediction(pred, y):
plt.figure()
plt.scatter(X, Y)
plt.scatter(X, pred)
plt.show()
# 경사 하강법 구현
W = np.random.uniform(-1, 1)
b = np.random.uniform(-1, 1)
learning_rate = 0.7 # 임의
for epoch in range(100):
Y_pred = W * X + b # 예측값
error = np.abs(Y_pred - Y).mean()
if error < 0.001:
break
# gradient descent 계산 (반복할 때마다 변경되는 W, b값)
w_grad = learning_rate * ((Y_pred-Y) * X).mean()
b_grad = learning_rate * ((Y_pred-Y)).mean()
# W, b 값 갱신
W = W - w_grad
b = b - b_grad
# 실제값과 예측값이 얼마나 근사해지는지 epoch % 5 ==0 될 때마다 그래프 그림
if epoch % 5 == 0:
Y_pred = W * X + b
plot_prediction(Y_pred, Y)
[파랑: 실제값, 주황: 예측값]
- 반복문이 실행되면서 오차가 점차 작아짐을 알 수 있음
- 최종적으로 오차가 줄어들며 실제값을 정확히 추정할 수 있음!
6. 다항 회귀
- 다항식을 사용한 선형 회귀
- y = a * x² + b * x + c 에서 x²을 z로 치환하면 y = a * z + b * x + c라는 선형식으로 쓸 수 있음
=> 다항식을 이용해서도 선형 회귀를 할 수 있음 → 최적의 곡선 찾기
- 비선형성을 띄는 데이터도 선형 모델을 활용하여 학습시킬 수 있다는 것
- 다항 회귀 기법: log, exp, 제곱 등을 적용해 선형식으로 변형한 뒤 학습시키는 것

# 50cm 농어 평균 무게 예측
# 훈련 세트, 테스트 세트의 길이를 제곱한 값의 열 추가 - 새로운 훈련, 테스트 세트 생성
train_poly = np.column_stack((train_input**2, train_input))
test_poly = np.column_statck((test_input**2, test_input))
# 새로운 훈련 세트, 테스트 세트로 선형 회귀 모델 훈련
lr = LinearRegression()
lr.fit(train_poly, train_target)
# 무게 예측
print(lr.predict([50**2, 50]))
# [1573.98423528]
7. 다항 회귀 구현
1) 회귀 다항식 y = a * x² + b * x + c 구하기
print(lr.coef_, lr.intercept_)
# [1.01433211 -21.55792498] 116.05021078278259=> 회귀 다항식) 무게 = 1.01 * 길이² - 21.6 * 길이 + 116.05
2) 훈련 세트의 산점도, 회귀 다항식 그리기
# 훈련 세트 산점도
plt.scatter(train_input, train_target)
point = np.arange(15, 50)
# 15~49까지 회귀 다항식 그래프 그리기
plt.plot(point, 1.01*point**2 -21.6*point + 116.05)
# 농어 데이터 표시하기
plt.scatter(50, 1574, marker = '^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
# 결정 계수
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))
# 0.9706807451768623
# 0.9775935108325121- 결정 계수 점수가 1에 근접하므로, 해당 모델은 위의 선형 모델보다 정확성이 높음
'ML & DL' 카테고리의 다른 글
| [BITAmin] K-최근접 이웃 알고리즘 (2) | 2023.01.23 |
|---|---|
| [BITAmin] 데이터 전처리 (0) | 2023.01.23 |