[수업출처] 숙명여자대학교 소프트웨어학부 유석종 교수님 자료구조 수업
1. Python
- Interpreter
- 객체 지향 Object-oriented
- 자료형 미리 선언하지 않음 Dynamic typing
- Sequence, collection data type
- 값 저장X, 참조 방식 Literal reference
- 동적 할당 Dynamic allocation
- 파이썬의 모든 변수 → 포인터
- 값에 대한 참조 변수 (값이 저장되어 있는 곳의 주소 참조)
- a, b = b, a : swap

2. Data type
1) Immutable data type 불변자료형
- int, float, string
- 값 변경 불가능 → 값 변경이 아니고 새로운 literal 참조하는 것
- 매개변수 전달시 값 변경 불가능


2) Mutable data type 가변자료형
- list, dictionary
- 원소 값 변경, 추가 가능
- 리스트는 각 원소 값에 대한 참조들의 모음
- 매개변수 전달시 인수 값 변경될 수 있음
- 가변자료형: '참조변수'를 바꿀 수 있다는 것


3. Parameter Passing
- call by value
- call by reference
- python → call by object reference 객체 참조 전달
def f(a):
a = 3
print(a)
return(a)
b = 2
f(b) # 3
print(b) # 2
b = f(b) # 3
print(b) # 3return을 받으려면 변수에 입력해야함
4. Alias 별명
- 두 변수가 하나의 객체를 동시에 참조하여 공유하는 것
A = [[2, 3, 4], 5]
B = A
B[0][1] = 'f'
print(A, id(A)) # [[2, 'f', 4], 5] 1860139826944
print(B, id(B)) # [[2, 'f', 4], 5] 1860139826944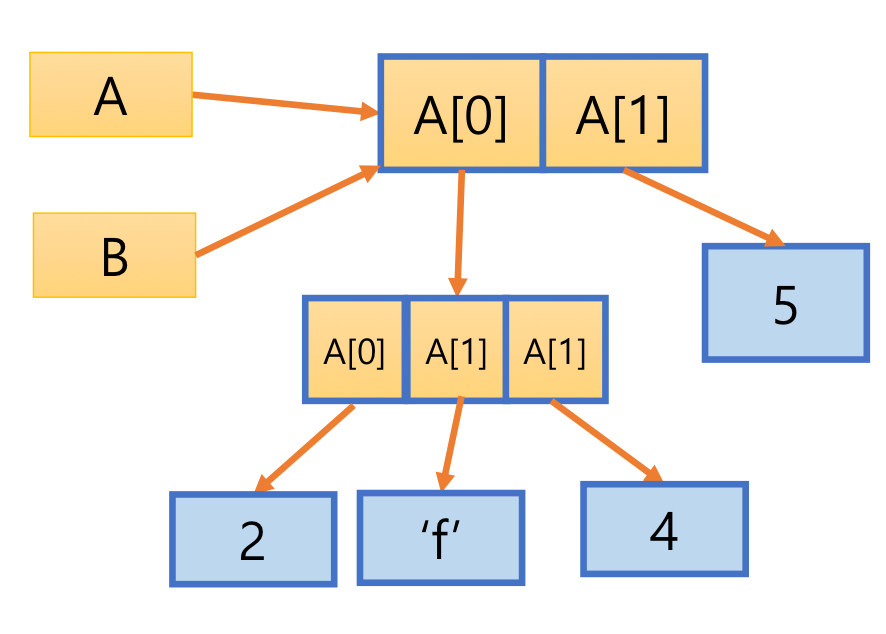
5. Shallow copy 얕은 복사
- 변수는 복사하여 새로 생성하지만 참조하는 리터럴은 공유하는 복사 방법
- copy 모듈의 copy() 함수로 실행
- 첫번째 level 객체만 복사
import copy
A = [[2, 3, 4], 5]
B = copy.copy(A) # B = list(A)
B[0][1] = 'f'
B[1] = 7
print(A, id(A), id(A[0]), id(A[0][1])) # [[2, 'f', 4], 5] 1860140611008 1860140611584 1860137884464
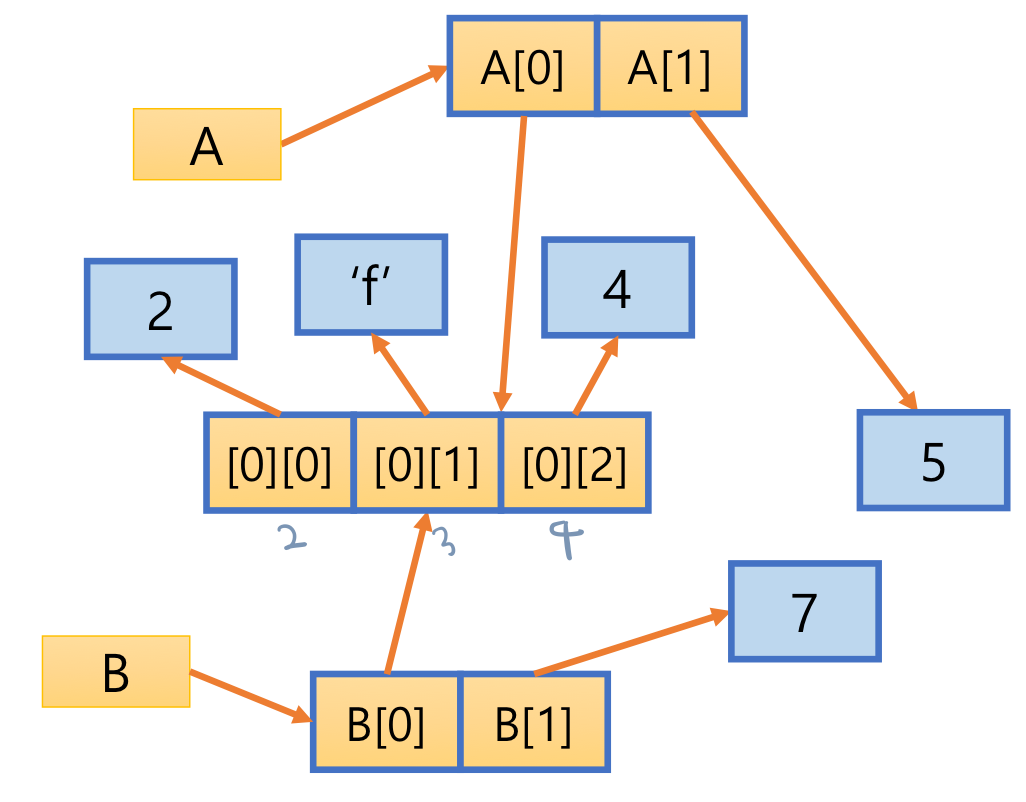
print(B, id(B), id(B[0]), id(B[0][1])) # [[2, 'f', 4], 7] 1860140611904 1860140611584 1860137884464- list A를 변수 B에 얕은 복사
- list B의 원소들은 새롭게 생성되지만, 원소들이 참조하는 객체는 원본과 동일하며 새로 생성되지 않음
- list A 와 B의 주소는 다르지만 리스트 원소가 참조하는 객체는 동일
6. Deep copy 깊은 복사
- 변수와 대상 객체(리터럴)를 모두 복제하여 생성
- 완전히 독립됨
import copy
A = [[2, 3, 4], 5]
B = copy.deepcopy(A)
B[0][1] = 'f'
B[1] = 7
print(A, id(A), id(A[0]), id(A[0][1]), id(A[1])
# [[2, 3, 4], 5] 1482518103488 1482518184832 1482509412720 1482509412784
print(B, id(B), id(B[0]), id(B[0][1]), id(B[1])
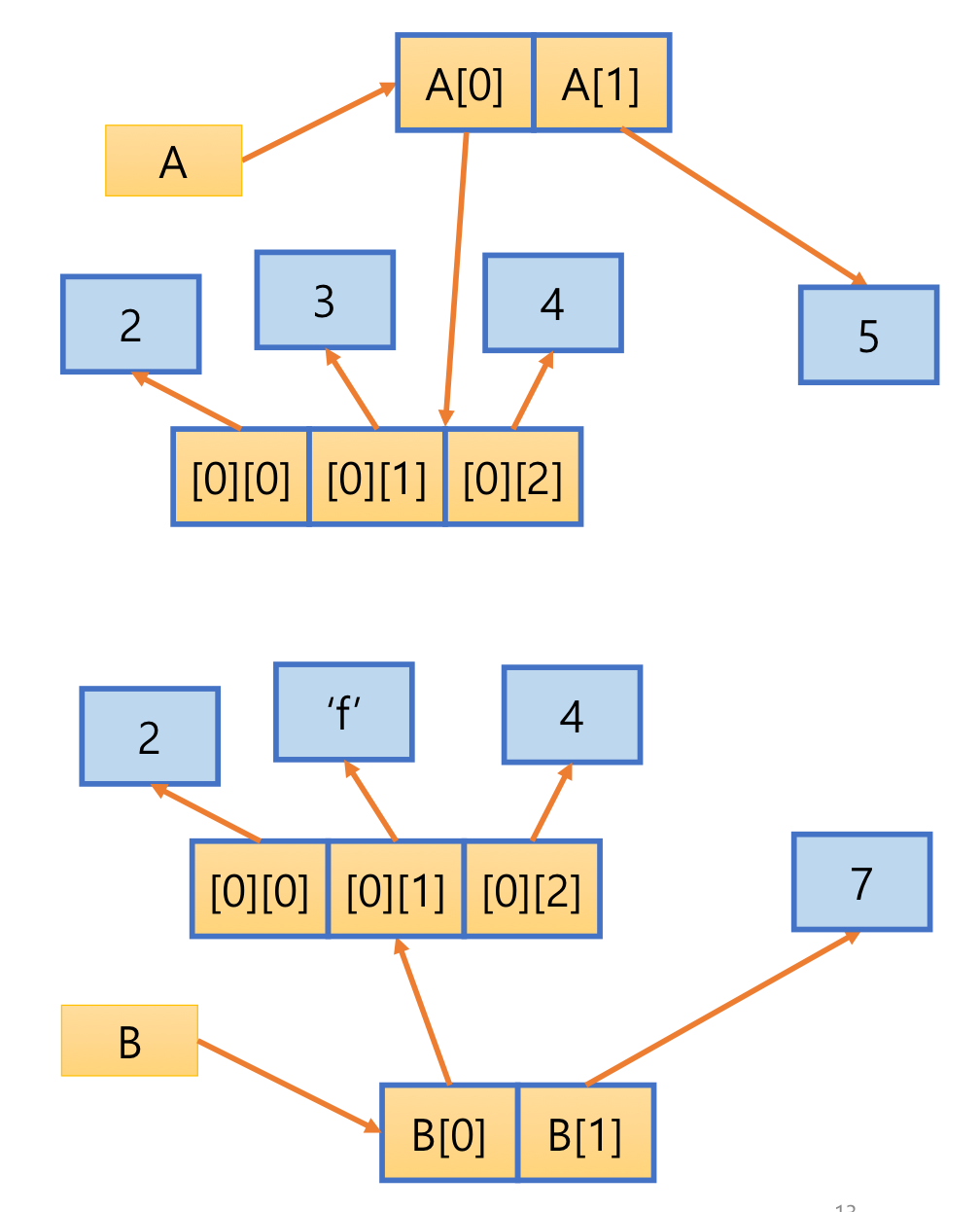
# [[2, 3, 4], 5] 14825181072000 1482518204544 1482509753136 1482509412848- 변수 A와 B, 리스트 원소, 원소가 참조하는 객체의 주소가 모두 다름
- 리스트 원소가 참조하는 객체도 복제되기 때문에 B의 원소 값을 수정해도 리스트 A가 참조하는 객체에는 변화가 없음
7. List
- 원소의 자료형 같을 필요 없음
- 파이썬은 정적 배열 지원하지 않음
- 사이즈는 고정되어 있지 않음 dynamic
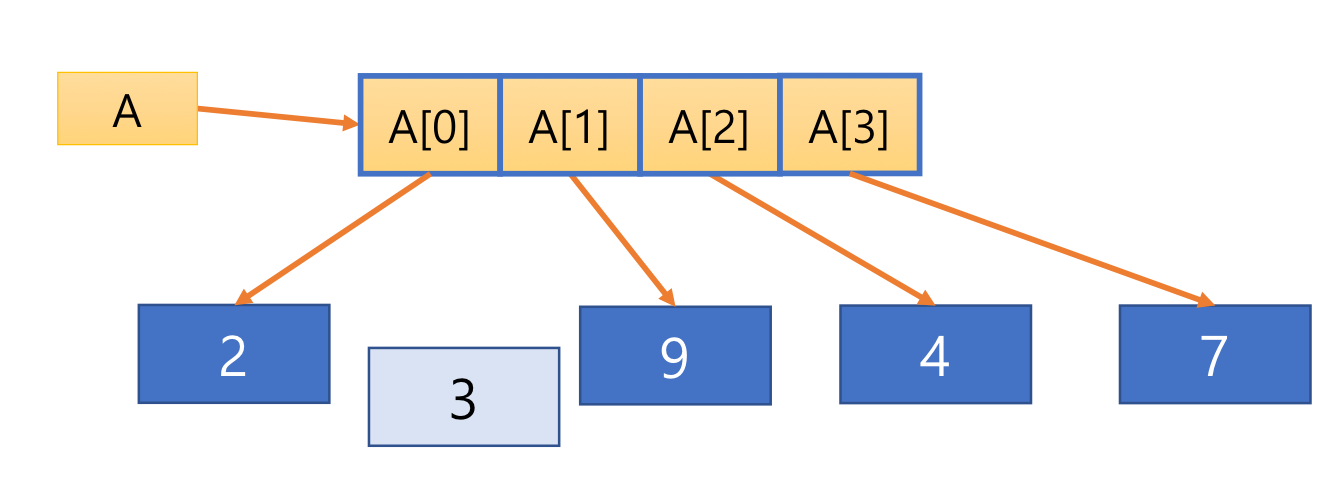
- referential array 리스트 원소는 값에 대한 참조 변수
A = [2, 3, 4]
A.append(7)
A[1] = 9
1) 리스트 생성
- 리스트 복합 표현
- range(), list() 함수 사용
- 빈 리스트 선언 후 원소 추가
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
num1 = [i for i in range(10)]
num2 = list(range(10))
num3 = []
for i in range(10):
num3 = num3 + [i] # num3.append(i)
2) 주사위 던지기 예제
import random
def throw_dice(count, n):
for i in range(n):
eye = random.randint(1, 6)
count[eye-1] += 1
def calc_ratio(count):
ratio = []
total = sum(count)
for i in range(6):
ratio.append(count[i]/total)
return ratio
def print_percent(num):
print('[', end = '')
for i in num:
print('%4.2f %i, end = ' ')
print(']')dice = [0]*6
for n in [10, 100, 1000]:
print('Times = ', n)
throw_dice(dice, n)
print(dice)
ratio = calc_ratio(dice)
print_percent(ratio)
print()Times = 10
[2, 1, 2, 1, 2, 2]
[0.20, 0.10, 0.20, 0.10, 0.20, 0.20]
Times = 100
[17, 14, 24, 28, 16, 21]
[0.15, 0.13, 0.22, 0.16, 0.15, 0.19]
Times = 1000
[197, 185, 176, 162, 188, 202]
[0.18, 0.17, 0.16, 0.15, 0.17, 0.18]
3) 2차원 배열 생성
scores = [[75, 90, 85], [60, 100, 75], [90, 70, 80]]
print('scores', scores)
for score in scores:
for num in score:
print(num, end = ' ')
print()
print()
print('scores[0][1]', scores[0][1])
print('scores[2]', scores[2])
print('scores[2][2]', scores[2][2])scores [[75, 90, 85], [60, 100, 75], [90, 70, 80]]
75 80 85
60 100 75
90 70 80
scores[0][1] 90
scores[2] [90, 70, 80]
scores[2][2] 80
4) 볼링 점수 계산 예제
score1 = [(8,0), ((4,3), (8,2), (4,6), (2,6), \
(10,0), (9,0), (10,0), (8,2), (10,0), (10,10)]
score2 = [(10,0), (10,0), (10,0), (10,0), (10,0), \
(10,0), (10,0), (10,0), (10,0), (10,0), (10, 10)]
score_list = [score1, score2] # 첫번째, 두번째 게임
for score in score_list:
i = total = 0
frame = [] # (프레임 점수, 결과)
for first, second in score: # 1회, 2회 쓰러뜨린 핀의 수
f_total = first + second
next_first, next_second = score[i+1]
if first == 10:
result = 'STRIKE'
f_total += next_first + next_second
# 1~9 프레임에서 더블을 친 경우
if i != 9 and next_first == 10:
next_next_first, next_next_second = score[i+2]
f_total += next_next_first
elif (first + second) == 10:
result == 'SPARE'
f_total += next_first
else: result = 'NONE'
total += f_total
frame.append((f_total, result))
i += 1
if i == 10: break
print(frame)
print('Total = ', total)
print()[(8, 'NONE'), (7, 'NONE), (14, 'SPARE'), (12, 'SPARE'), (8, 'NONE'), (19, 'SPARE'), (9, 'NONE'), (20, 'STRIKE'), (20, 'SPARE'), (30, 'STRIKE')]
Total = 147
[(30, 'STRIKE'), (30, 'STRIKE'), (30, 'STRIKE'), (30, 'STRIKE'), (30, 'STRIKE'), (30, 'STRIKE'), (30, 'STRIKE'), (30, 'STRIKE'), (30, 'STRIKE'), (30, 'STRIKE')]
Total = 300
8. Set and Dictionary
1) Set
- 수학의 집합과 유사한 자료구조로 집합 연산자 지원
- 원소의 나열 순서가 없으며 중복 허용하지 않음
- s1 = set([1, 2, 3])
- s2 = {2, 3, 4}
- 연산자
- membership( in ), 합집합 union( | ), 차집합 difference( - )
- add()
- update( { } )
- remove()
2) Dictionary
- key & value의 쌍으로 구성된 자료형
- 키를 통해 원소에 접근
- items() : 각 항목 튜플로 반환
- keys() : 키만을 추출하여 리스트로 반환
- values() : 값만을 추출하여 리스트로 반환
- 단어 출현 빈도 예제
sentence = sentence.lower() # 소문자로 변환
words = sentence.split() # 단어 단위로 분리
dic = {}
for word in words:
if word not in dic:
dic[word] = 0
dic [word] += 1
print('# of different words =', len(dic))
n = 0
for word, count in dic.items():
print(word, '(%d)' %count, end = ' ')
n += 1
if n % 3 == 0: print()# sentence = 'Van Rossum was born and raised in the Netherlands, where he received a master's degree in mathematics and computer science from the University of Amsterdam in 1982. In December 1989, Van Rossum had been looking for a hobby programming project that would keep him occupied during the week around Christmas as his office was closed when he decided to write an interpreter for a new scripting language he had been thinking about lately, a descendant of ABC that would appeal to Unix / C hackers. '
# of different words = 66
van (2) rossum (2) was (2) born (1) and (2) raised (1) ...
9. Polynomial ADT 다항식 객체 (추상자료형)
- polynomial A(x) = 3x^20 + 2x^5 + 4
- x: variable, a: 계수 coefficient, e: 지수 exponent
- 튜플로 저장해야할 것: coefficient, exponent
# 다항식 덧셈
def padd(a, b, d):
while a and b:
coef1, exp1 = a[0]
coef2, exp2 = b[0]
if exp1 > exp2:
d.append(a.pop(0))
elif exp1 < exp2:
d.append(b.pop(0))
else:
if coef1 + coef2 == 0:
a.pop(0)
b.pop(0)
else:
d.append((coef1 + coef2, exp1))
a.pop(0)
b.pop(0)
for coef, exp in a:
d.append((coef, exp))
for coef, exp in b:
d.append((coef, exp))a = [(5, 12), (-6, 8), (13, 3)]
b = [(10, 15), (4, 8), (9, 0)]
d = []
padd(a, b, d)
print(d)
# [(10, 15), (5, 12), (-2, 8), (13, 3), (9, 0)]
10. Sparse Matrix 희소 행렬
- 2D array: matrix[m][n] → 공간복잡도 S(m, n) = m*n
- Sparse matrix A[m, n] : 유효한 값은 거의 없고 나머지는 0인 행렬
- 2D array에 저장하기에 메모리 공간이 아까운 경우 → 0이 아닌 값 저장 (행, 열, 값)
- a[0].row: 행렬의 행 수
- a[0].col: 행렬의 열 수
- a[0].value: 0이 아닌 값의 개수
- a[1]부터 0이 아닌 값의 행, 열, 값 저장 (left-right, top-bottom)

class SparseMatrix:
def __init__(self):
self.matrix = [[15, 0, 0, 22, 0, 15], \
[0, 11, 3, 0, 0, 0], \
[0, 0, 0, -6, 0, 0], \
[0, 0, 0, 0, 0, 0], \
[91, 0, 0, 0, 0, 0], \
[0, 0, 28, 0, 0, 0]]
self.sparse_list = []
def toTuple(self):
row = count = 0
for rows in self.matrix:
col = 0
for value in rows:
if value != 0:
count += 1
self.sparse_list.append((row, col, value))
count += 1
row += 1
height = len(self.matrix)
width = len(self.matrix[0])
self.sparse_list.insert(0, (height, width, count))s = SparseMatrix()
s.toTuple()
print(s.sparse_list)
# [(6, 6, 8), (0, 0, 15), (0, 3, 22), (0, 5, 15),
# (1, 1, 11), (1, 2, 3), (2, 3, -6), (4, 0, 91), (5, 2, 28)]
'Software > Data Structures' 카테고리의 다른 글
| [Python] 2장 연습문제 (0) | 2022.04.16 |
|---|---|
| [Python] 1. Introduction (0) | 2022.03.08 |
| [자료구조] 탐색 (0) | 2021.04.20 |
| [자료구조] 연결 리스트 (0) | 2021.04.20 |
| [자료구조] 선형 자료구조 (0) | 2021.04.18 |