1. 데이터 전처리
- 특정 분석에 적합하게 데이터를 가공하는 작업
- 완결성: 필수로 기입되어 있어야 하는 데이터는 모두 입력되어야 한다.
- 유일성: 동일한 데이터가 불필요하게 중복되어 있으면 안된다.
- 통일성: 데이터가 모두 동일한 형식으로 입력되어야 한다.
2. 주의해야 하는 점
- 잡음 Noise: 측정 과정에서 무작위로 발생하여 측정값의 에러를 발생시키는 것. 이상치와 달리 예측하기 어려움
- 아티펙트 Digital Artifact: 어떤 기술적인 요인으로 인해 반복적으로 발생하는 왜곡이나 에러
- 정밀도 Precision: 동일한 대상을 반복적으로 측정했을 때, 각 결과의 친밀성을 나타내는 것. 측정 결과의 표준편차로 표현 가능
- 편향 bias: 측정 장비에 포함된 시스템적인 변동 (ex. 영점 조절이 되지 않은 체중계)
- 정확도 Accuracy: 평향에 영향 받음. 유효 숫자의 사용에 있어서 중요함
- 이상치 Outlier: 대부분의 데이터와 다른 특성을 보이너가, 특정 속성의 값이 다른 개체들과 달리 유별난 값을 가지는 데이터. 잡음과 다름
- 결측치 Missing Value: 값이 표기되지 않은 값
- 모순, 불일치 Inconsistent Value: 동일한 개체에 대한 측정 데이터가 다르게 나타나는 경우
- 중복 Duplicated data: 중복된 데이터 사이에 속성의 차이나, 값의 불일치가 발생하면 문제가 됨
3. 전처리 순서
1) 데이터 수집: 분석이나 학습에 필요한 데이터를 수집하는 작업
- 데이터 분석 및 모델 생성의 첫 과정
- 목적에 맞는 정보 수집을 위해 문제 정의 필요
2) 데이터 정제: 비어있는 데이터나 잡음, 모순된 데이터를 정합성이 맞도록 교정하는 작업
- 데이터를 활용할 수 있도록 만드는 과정
- 컴퓨터가 읽을 수 없는 요소의 제거 및 숫자나 날짜 등의 형식에 대해 일관성 유지
- 누락값, 불일치 값, 오류 값 수정
3) 데이터 통합: 여러 개의 데이터 베이스, 데이터 집합 또는 파일을 통합하는 작업
- 서로 다른 데이터 세트가 호환이 가능하도록 통합
- 같은 객체, 같은 단위나 좌표로 통합
4) 데이터 축소: 샘플링, 차원 축소, 특징 선택 및 추출을 통해 데이터 크기를 줄이는 작업
- 대용량 데이터에 대한 복잡한 데이터 분석은 실행하기 어렵거나 불가능한 경우가 많음
5) 데이터 변환: 데이터를 정규화, 이산화 또는 집계를 통해 변환하는 작업
4. 데이터 전처리 기법
- 집계 Aggregation
- 샘플링 Sampling
- 차원 축소 Dimensionality Reduction
- 특징 선택 Feature Subset Selection
- 특징 생성 Feature Creation
- 이산화와 이진화 Discretization and Binarization
- 속성 변화 Attribute Transformation
5. 전처리 전 데이터 확인
- shape: 데이터 크기 출력
- head(): 데이터 상위 5개 행 출력
- tail(): 데이터 하위 5개 행 출력
- info(): 데이터 전반적인 정보 제공 (행/열 크기, 컬럼명, 컬럼을 구성하는 값의 자료형 등)
- describe(): 데이터 컬럼별 요약 통계량 제공
6. 결측치 처리
- NA : 값이 표기되지 않은 값. 결측치
- 제거, 대치, 예측모델로 처리
1) 전체 결측치 확인
df.isnull()
pd.isnull(df)
# 결측치일 때 true 반환
# isnull -> notnull : 결측치일 때 false 반환
2) 인덱싱 후 결측치 개수 확인하기
df['col'].isnull()
3) 결측치 만들기
df.ix[[row1, row2], ['col']] = None
4) 전체 결측치 개수 확인
df.isnull().sum()
df.isnull().value_counts()
df.isnull().sum(1)
5-1) 결측치 제거
- dropna() : 판다스에서 누락 데이터를 제거하는 함수
- 목록삭제 : 결측치가 있는 행/열은 전부 삭제
df = df.dropna() # default, 행 제거
df = df.dropna(axis = 1) # 열 제거
- 단일값 삭제 : 행/열 자체가 결측치일 때, 혹은 조건부 삭제
df = df.dropna(how = 'all')
df = df.dropna(thresh = 1)
df = df.dropna(subset=['col1', 'col2', 'col3'], how = 'all') # 모두 결측치일 때 해당 행 삭제
df = df.dropna(subset=['col1', 'col2', 'col3'], thresh = 2) # 특정 열에 2개 초과의 결측치가 있을 때 해당 행 삭제
5-2) 대치
- 단순 대치: 중앙값, 최빈값, 0, 분위수, 주변값, 예측값 등으로 결측치 대치
- 다중 대치: 단순 대치법을 여러번! (대치 - 분석 - 결합)
- 판다스에서 결측치 대치하는 함수들
fillna()
# 전체 결측치를 특정 단일값으로 대치
df.fillna(0)
# 특정 열에 결측치가 있을 경우 다른 값으로 대치
df['col'] = df['col'].fillna(0)
df['col'] = df['col'].fillna(df['col'].mean())
# 결측치 바로 이후 행 값으로 채우기
df.fillna(method='bfill')
# 결측치 바로 이전 행 값으로 채우기
df.fillna(method='pad')replace()
# 결측치 값 0으로 채우기
df.replace(to_replace = np.nan, value = 0)interpolate()
# 인덱스를 무시하고, 값을 선형적으로 같은 간격으로 처리
df.interpolate(method = 'linear', limit_direction = 'forward')
5-3) 예측 모델
- 결측값을 제외한 데이터로부터 모델을 훈련하고 추정값을 계산하고 결측치 대체
- K-NN, 가중 K-NN, 로지스틱 회귀, SVM, 랜덤 포레스트 방식 등
7. 중복 데이터 처리
- 중복은 언제든지 발생할 수 있지만, 중복 데이터 사이에 속성의 차이나 값의 불일치가 발생한 경우, 처리해야 함
- 두 개체를 합치거나 응용에 적합한 속성을 가진 데이터를 선택하는 등
# 중복 데이터 확인
df.duplicated(['col'])
# 중복 데이터 삭제
drop_duplicates()
# 해당 열의 첫 행을 기준으로 중복 여부 판단 후, 중복되는 나머지 행 삭제
drop_duplicated(['col'])
df.drop_duplicates(keep = )
subset = None # default, 특정 열 지정 X, 모든 열에 대해 작업 수행
keep = 'first' # 가장 처음에 나온 데이터만 남김
keep = 'last' # 가장 마지막에 나온 데이터만 남김
keep = False # 중복된 어떤 데이터도 남기지 않음
8. 불균형 데이터 처리
- 분류를 목적으로 하는 데이터 셋에 클래스 라벨의 비율이 불균형한 경우
- 각 클래스에 속한 데이터 개수 차이가 큰 데이터
- 정상 범주의 관측치 수와 이상 범주의 관측치 수가 현저히 차이나는 데이터
- 이상 데이터를 정확히 찾아내지 못할 수 있음
8-1) Under Sampling
- 다수 범주의 데이터를 소수 범주의 데이터 수에 맞게 줄이는 샘플링 방식
- Random Undersampling, Tomek's Link, CNN
8-2) Over Sampling
- 소수 범주의 데이터를 다수 범주의 데이터 수에 맞게 늘리는 샘플링 방식
- Random Oversampling
- ADASYN, SMOTE
9. 이상치 탐지 기법
1) z-score
- z = (x - μ) / σ
- 변수가 정규분포 따른다고 가정, 각 특성값이 평균에서 표준편차의 몇 배만큼 떨어져 있는지 나타냄
- z-score가 임계치보다 크거나 작은 관측치를 이상치라고 규정
- 임계치 조정함으로써 기준 조정
def z_score_outlier(df, col, thres = 3):
z_score = (df[col] - df[col].mean()) / df[col].std()
return df[(z_score > thres) | (z_score < -thres)]
2) IQR
- IQR = Q3 - Q1
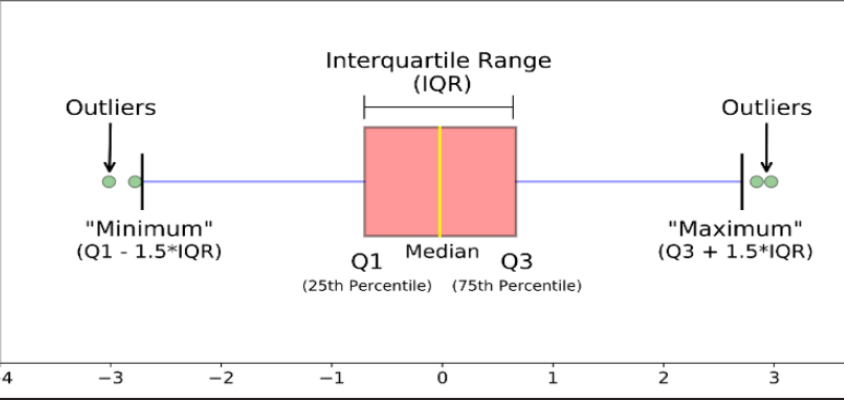
- Q3 + 1.5*IQR 이상이거나, Q1 - 1.5*IQR 이하인 경우 이상치라고 규정
- 1.5 대신 다른 값 이용해 기준 조정 가능
def IQR_outlier(df, col, scale = 1.5):
Q1 = df[col].quantile(0.25)
Q3 = df[col].quantile(0.75)
IQR = Q3 - Q1
lower_limit = Q1 - scale * IQR
upper_limit = Q3 + scale * IQR
return df[(df[col] > upper_limit) | df[col] < lower_limit)]
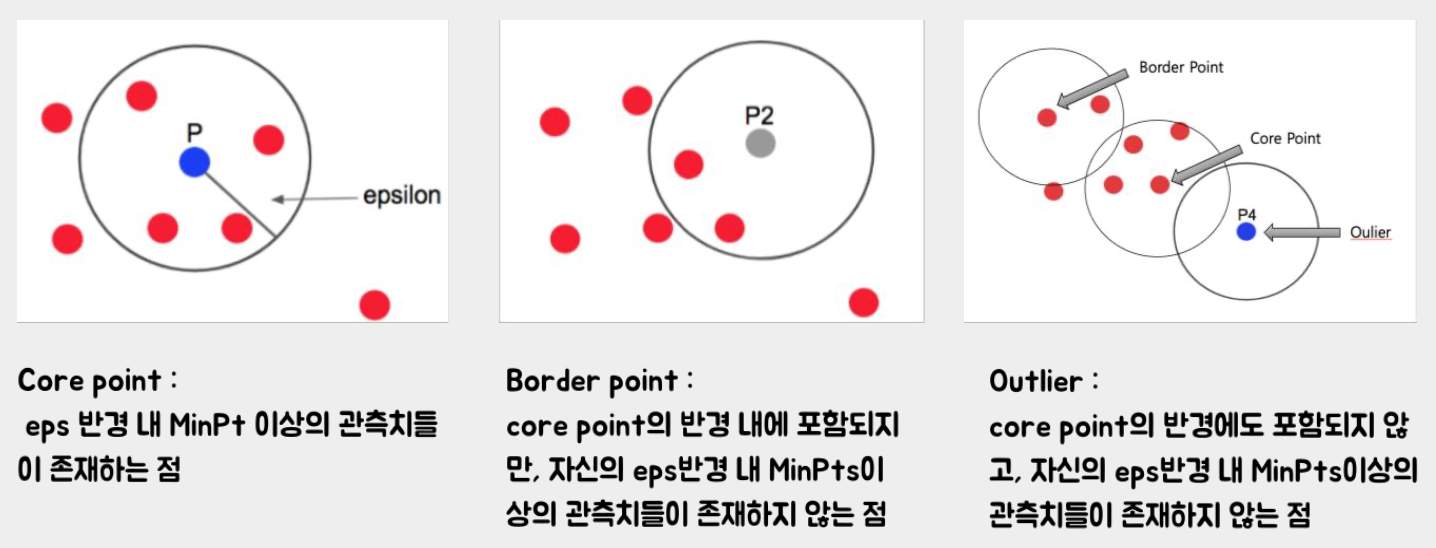
3) DBSCAN
- 밀도 기반 군집화 알고리즘
- 하이퍼 파라미터: eps(반경, default=0.5), min_samples(core point가 되기 위한 최소한의 이웃 수, default=5)
# 이상치 탐지
from sklearn.cluster import DBSCAN
model = DBSCAN(eps = .3, min_samples = 10)
pred = model.fit_predict(abalone)
# 이상치 개수
(pred == -1).sum()
10. 레이블 인코딩
- 문자열 카테고리 피처를 코드형 숫자 값으로 변환하는 것
# pandas
df.factorize()
# scikit-learn
LabelEncoder()
encoder.fit_transform() # 학습, 변환 한번에
11. 원핫 인코딩
- 피처값의 유형에 따라 새로운 피처를 생성해 고유값에 해당하는 컬럼에만 1 표시, 나머지 컬럼에는 0을 표시하는 방식
- 숫자의 크기 차이를 만드는 레이블 인코딩의 단점 보완
12. Feature Scaling
- 서로 다른 변수 값의 범위를 일정한 수준으로 맞추는 작업
- 변수 값의 범위 또는 단위가 달라서 발생 가능한 문제 예방
- 머신러닝 모델이 특정 데이터의 bias 갖는 것 방지
1) 표준화 Standardization
- 서로 다른 범위의 변수들을 평균이 0이고 분산이 1인 가우시안 정규분포를 가진 값으로 변환
- ScandardScaler()
2) 정규화 Normalization
- 변수값들을 모두 0과 1 사이의 값으로 변환하는 방식
- MinMaxScaler()
'ML & DL' 카테고리의 다른 글
| [BITAmin] 선형 회귀 (0) | 2023.01.23 |
|---|---|
| [BITAmin] K-최근접 이웃 알고리즘 (2) | 2023.01.23 |