수업 출처) 숙명여자대학교 소프트웨어학부 수업 "데이터사이언스개론", 박동철 교수님
1. Predictive Modeling 예측 모델
- 일반적인 절차
- training data를 가장 잘 표현하는 모델 설정
- 새로운 데이터에 모델 적용하여 결과 예측
- 아마 처음으로 classification을 생각할 것이다.
- 새로운 데이터가 어느 클래스에 속할지 training dataset을 기반으로 확인한다.
- (ex) 이 고객이 회사를 금방 떠날 것 같은가? → YES / NO
2. Model
- 현실을 목적에 맞는 것만 남도록 간략하게 표현한 것이다.
- 중요한 것과 중요하지 않은 것을 기반으로 간략화한다.
- 부적절한 정보는 날리고 관련이 있는 데이터들만 남긴다.
- (ex) 지도, 청사진
2-1. Predictive Model
- 타겟에 대해 모르는 값을 추정하는 공식이다.
- 예측의 정확도로 성능을 평가한다.
- 수학적인 표현(ex: linear regression)과 논리적인 표현(ex: decision tree)이 있다.
2-2. Descriptive Model
- 데이터에 내재되어 있는 인사이트를 얻는 것이 주 목적인 모델이다.
- 즉, 예측"값"을 얻는 것이 목적이 아니다.
- 예시로는 clustering, profiling 등이 있다.
- 도출된 지능과 이해가능성으로 성능을 평가한다.
- 많은 모델들이 두가지 목적을 모두 제공할 수 있다.
3. Model Induction 모델 유도
- 데이터로부터 모델 유도
- 특정한 사례를 일반적인 규칙으로 일반화하는 것이다.
- 모델은 통계학적 의미에서 일반적인 규칙이다.
- 항상 100% 맞진 않는다.
- Induction algorithm 유도 알고리즘 (leaner) : 데이터로부터 모델을 형성하기 위한 절차이다.
- Training data 훈련 데이터 (labeled data) : 모델을 유도하기 위해 유도 알고리즘에 대입하는 데이터이다. 이미 라벨 값을 알고있다.
4. Supervised Segmentation 지도 분할
4-1. Basic idea
- 타겟에 대해 서로 다른 값들을 갖는 하위 그룹으로 분할하는 방법이다.
- 즉, 그룹끼리는 타겟에 대해 같은 (비슷한) value를 가진다.
- 분할에 사용된 변수 (값, attribute) 를 예측의 타겟 속성으로 사용할 수 있다.
- 데이터를 가장 잘 분류할 수 있는 속성을 선택하는 것이 중요하다.
4-2. Selecting Information Attributes
- 효과적으로 데이터를 분류하기 위해서는 유용한 속성을 사용해야 한다.
- 유용한 속성은 해당 변수에 대해 중요한 값을 갖는 속성이다.
- 즉, 타겟의 값을 예측하는 것을 도와줄 수 있는 속성이다.
- (Ex)
- 사람들을 'yes' 와 'no'로 분류하고자 한다.
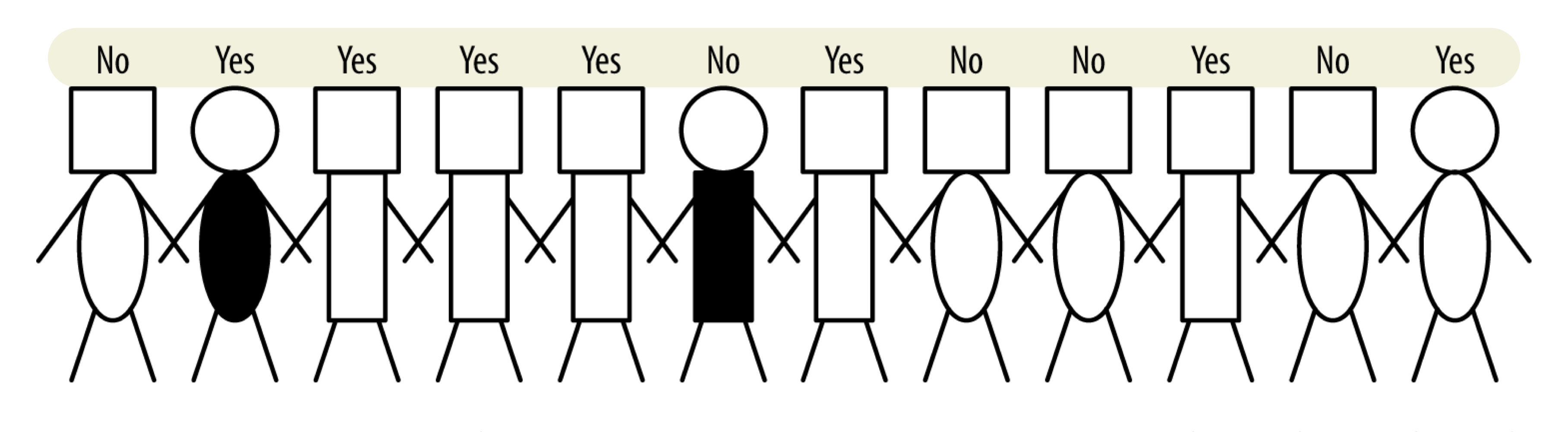
- 속성
- 머리 : 정사각형 / 원
- 몸 : 직사각형 / 타원
- 몸 색 : 검정 / 하양
- target variable : 체납 여부 - yes / no
- 어떤 속성이 사람들을 yes와 no로 가장 잘 분류할 수 있을까?
- 우리는 그룹을 가능한 pure하게 분류하고자 한다.
- pure
- 그룹이 타겟 값에 대해 동일한 값을 갖는 상태를 말한다.
- 하나의 멤버라도 다른 값을 가지면 그 그룹은 impure하다고 말한다.

- 문제
- 속성이 완벽하게 그룹으로 분리되는 경우는 거의 없다.

- 머리 모양과 몸 색을 각각 그룹을 분리한 결과이다. 어떤 속성이 더 그룹을 잘 분리한 것일까?
- 모든 속성이 위의 예제처럼 2가지로 나누어지는것은 아니다. 더 많은 경우에는 어떻게 분리할 수 있을까?
- (연속적인) 숫자 값을 가지는 속성은 어떻게 분류하는 것이 좋을까? (ex: 나이)
- 분류 기준
- 속성이 데이터를 얼마나 잘 분류하는지를 평가하는 공식을 만들 수 있다.
- 그 공식은 '순도'에 기반할 수 있다.
- Information Gain
- 가장 대표적인 분류 기준이다.
- 순도를 측정하는 "엔트로피"에 기반한다.
- Entropy 무질서도
- 무질서도를 측정하는 기준이다. 타겟의 관점에서 분류가 얼마나 impure하게 되었는지 측정한다.
- H(S) = Σ p𝑖 log₂ (1/p𝑖)
- p𝑖 : S에서 𝑖를 가질 확률 (Σ p𝑖 = 1)
- (Ex)
- attribute S = {yes, yes, yes, no, no} → p₁(yes) = 3/5, p₂(yes) = 2.5
- H(S) = 3/5 log₂(5/3) + 2/5 log₂(5/2) = 0.97 → very impure

4-3. Information Gain
- 엔트로피는 각각의 분할이 얼마나 impure한지만 측정한다.
- 즉, 한 개의 속성만 고려한다.
- information gain은 속성이 만드는 전체 분할에 대한 엔트로피 증감 정도를 측정한다.
- 엔트로피가 감소하면 유용한 정보이고, 엔트로피가 증가하면 정보를 얻을 수 없는 속성으로 분할한 것이다.
- IG = H(parent) - [ Σ p(c𝑖) ·H(c𝑖) ]
- 각 child (분류된 그룹)에 대한 엔트로피는 각각의 그룹에 속하는 인스턴스의 비율에 가중된다.

- Information Gain 값이 클수록 유용한 속성이다.
4-4. Numerical Variables
- 회귀 문제와 같이 속성 값이 "숫자형"인 경우는 카테코리값을 가진 속성보다 분류하기 어렵다.
1) Discretize 이산화
- 한 개 이상의 분할점을 선택해서 숫자 값을 이산화하는 방법이다.
- 그 후 카테고리형 속성과 같이 다룰 수 있다.
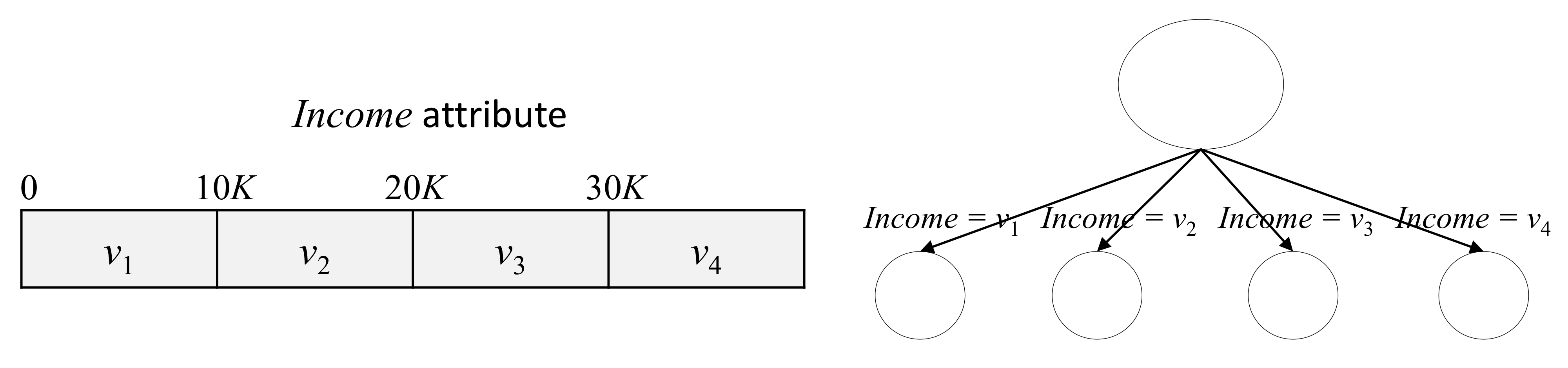
2) 여러 개의 후보 분할점을 고르는 방법
- 각각의 후보 분할점에 대해 IG 를 계산한 후 가장 IG 값이 큰 경우를 선택하는 방법이다.

5. Classificaiton Tree Segmentation
- 여러 개의 속성을 사용해서 데이터를 분류하는 방법이다. → 트리 모양

- structure
- interior node : 분류의 기준이 되는 속성 이름이다.
- leaf node : 분류된 class(결과?)를 말한다.
- branch : 속성의 구분되는 값을 말한다. (분류 기준, 범위)
- path from the root to a leaf : 분류의 특징을 설명하는 길이다.
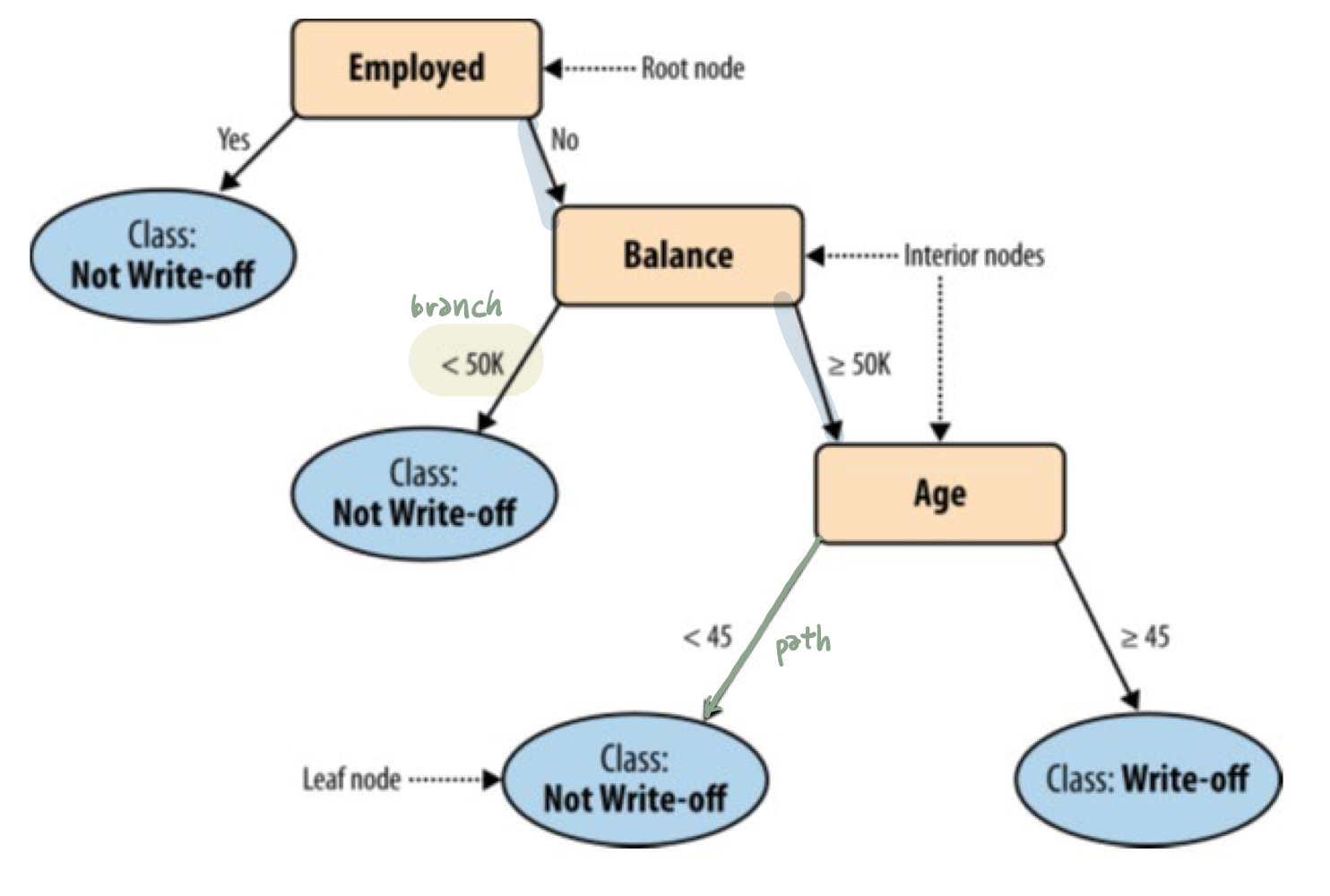
- procedure
- 분류 값을 모르는 예시들이 있다.
- root node에서부터 예시들의 특정 속성 값들로 branches를 선택하면서 interior nodes를 타고 내려온다.
- terminal node (leaf node)에 도달하면 그것은 분류가 된 것이다.
- (ex)
- balance = 115K, employed = no, age = 40 인 사람을 분류해보자.
- root node인 employed 부터 no, ≥50K, <45 path를 따라서 내려온다.
- 결과적으로 class = Not Write-off 로 특정된 leaf node에 도착한다.
- 따라서 우리는 그 사람이 체납하지 않을 것이라고 예측할 수 있다.
- divide-and-conquer approach
- 전체 데이터셋을 나누기 가장 좋은 속성을 찾는다.
- 각 서브 그룹에 대해서 재귀적으로 가장 좋은 속성들을 찾아나간다.

- (ex) 위의 사람모형 예시
- 일련의 과정에서 IG 값의 크기에 따라 큰 순서대로 몸 모양 - 몸 색 - 머리 모양 순으로 그룹을 분류한다.


그 결과 위와 같은 classification tree를 얻을 수 있다.
- 요약해보면, 데이터를 재귀적으로 나누는 과정이다.
- 각 과정에서 모든 속성을 테스트하고 그룹을 가장 순수하게 나누는 (IG값이 큰) 속성을 선택한다.
- 멈추는 단계는 모든 leaf node가 pure할 때, 변수를 끝까지 나눴을 때 등이 있지만, 이렇게까지 나누면 모델이 overfitting될 것이다.
6. Visualizing Segmentation
- classification tree 결과를 공간 상에 시각화할 때 사용한다.
- 하지만, 시각화는 두세개의 특징으로만 가능하다.
- 그럼에도 고차원 공간까지 적용할 수 있는 인사이트를 얻을 수 있다.
7. 규칙
- classification tree는 구현하기 쉽기 때문에 자주 사용되며, 수학적 공식이 그렇게 복잡하지 않다.
- 논리적 문장으로 classification tree를 구현할 수 있다.
- 각각의 path가 statement가 된다.
- 각 sement는 path와 "AND"로 구성된다.

8. 확률 추정
- 단순한 분류보다 확률 추정을 할 때
- (ex) he will not write-off → the probability of him writing-off = 40%
- ranking과 같이 더욱 정교한 의사결정을 해야할 때 사용할 수 있다.

- Frequency-based propbability estimation
- 확률을 추정하기 위해 각 leaf 에서의 개체 수를 사용한다.
- leaf에서 그에 해당하는 개체 (positive) 가 n개, 해당하지 않는 개체 (negative) 가 m개라면, 새로운 개체가 그에 해당할 확률은 n/(n+m)이 된다.

8-1. overfitting problem
- 개체 수가 아주 적은 분류 그룹의 확률은 굉장히 높아질 수 있다.
- (ex) 개체 수가 1개인 그룹은 무조건 100%가 나올텐데, 그것이 좋은 분류라고 할 수 있을까? - 다른 그룹의 개체 수가 나머지 99개인 경우?
8-2. Laplace correction 라플라스 보정
- 단순히 빈도를 계산하는 대신, 빈도수 기반 추정치의 smoothed된 버전을 사용하는 것이다.

- (ex) p₁ : 2 postitive, no negative, p₂ : 20 positive, no negative
- frequency-base : p₁ = p₂ = 1
- laplace correction : p₁ = 0.75, p₂ ≈ 0.95
- 개체 수가 증가할수록 라플라스 방정식은 빈도수 기반 측정값에 수렴한다.

'Software > Data Science Introduction' 카테고리의 다른 글
| [데이터사이언스개론] Similarity, Neighbors, Clusters (0) | 2021.06.04 |
|---|---|
| [데이터사이언스개론] Overfitting and Avoidance (0) | 2021.04.22 |
| [데이터사이언스개론] Fitting Model to data (0) | 2021.04.22 |
| [데이터사이언스개론] 비즈니스 문제와 데이터 사이언스 솔루션 (0) | 2021.04.15 |
| [데이터사이언스개론] Data Science (0) | 2021.04.15 |