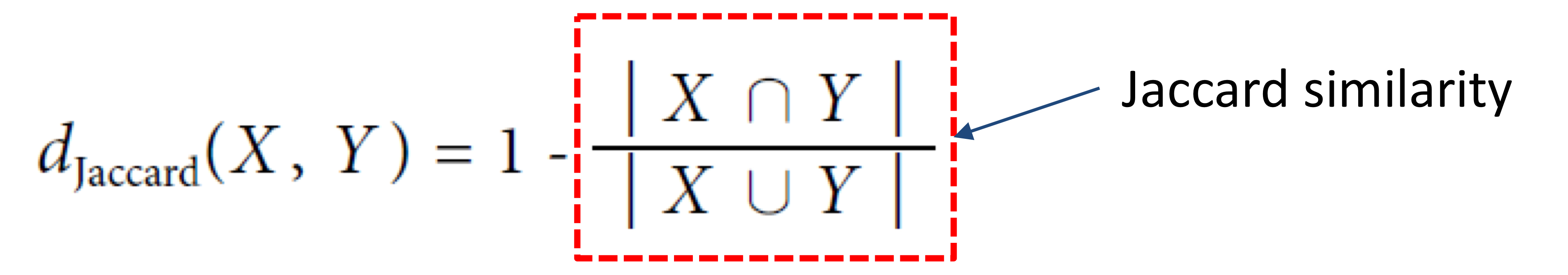수업 출처) 숙명여자대학교 소프트웨어학부 박동철 교수님, '데이터사이언스개론' 수업
1. how measure a model?
- 데이터 분석을 통해 "얻고싶은 것"이 무엇인지 신중히 고려하는 것이 중요하다.
- 모델의 수행 능력을 의미있는 방식으로 측정해야 한다.
- 각 문제에 대한 올바른 평가 방식은 무엇일까?
- ex) 이동통신사 고객 이탈 문제 (celluar-churn problem) : 정확한 예측의 비율? 이탈한 고객의 비율?
2. Evaluation Classifiers (예측모델 평가)
- 알지 못하는 클래스에 대해 이미 갖고 있는 데이터를 바탕으로 예측하는 모델이다.
- 이진 예측 모델의 클래스: positive / negative
- 이러한 모델이 얼마나 잘 수행되는지 어떻게 평가할 것인가?

2-1. Plain Accuracy
- 지금까지 우리는 classifier의 성능을 측정하기 위한 간단한 지표를 가정했다. : accuracy (or error rate)
- accuracy = 예측 중 맞은 개수 / 전체 개수 = 1 - error rate
- 측정하기 쉽고 이해하기 쉽기 때문에 많이 쓰이는 방법이다.
- 하지만, 너무 간단하고, 몇 개의 문제점들이 있다.
2-2. Confusion Matrix
- n개의 클래스를 분류하기 위한 n x n 행렬이다.
- 행(rows) : 예측값
- 열(columns) : 실제 값
- 다른 종류의 오차(error)들을 개별적으로 보여준다. : False positives, False negatives
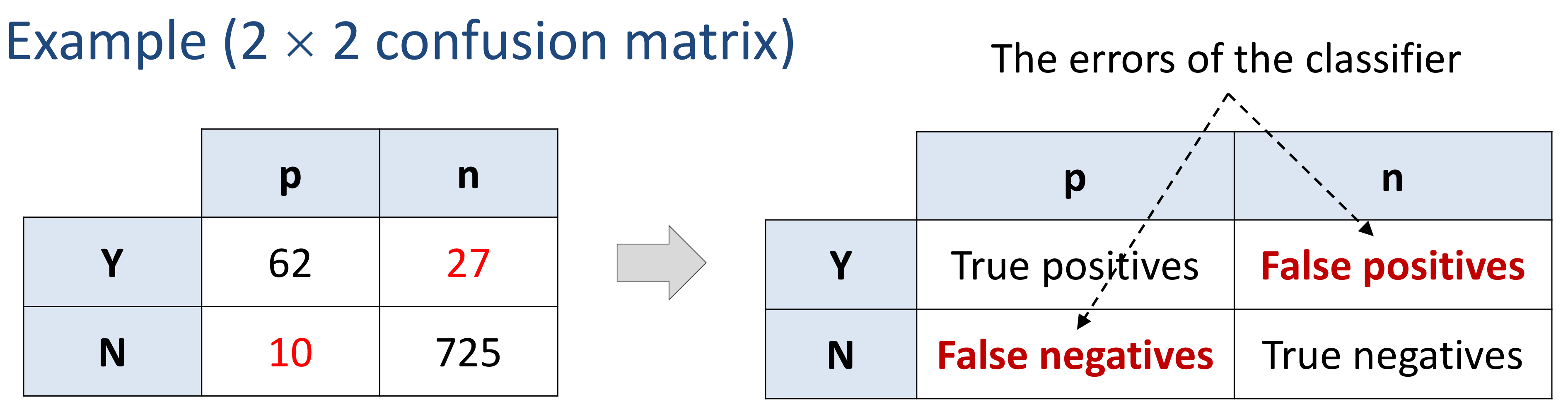
- p, n이 실제 클래스에 속하는 값들이고, y, n이 예측한 값들이다.
- 따라서 y-p에 속하는 값들은 y로 예측했는데 실제로 positive인 값들이다.
2-3. Problems with Unbalanced classes
1) 분류 문제에서 한 클래스가 rare하다고 생각해보자.
- 예를 들어, 사기당한 고객을 찾는 경우나, 결함이 있는 부품을 찾는 경우나, 광고 등에 응하는 고객을 찾는 경우 그런 경우들이 흔치 않기 때문에 클래스 분포가 불균형하거나 비스듬할 것이다.
- 이러한 경우에는 accuracy로 성능을 판단하기 어렵다.
- 예를 들어 클래스 값이 999:1 비율이라면, 항상 999의 개체가 속한 클래스를 선택한다면 정확도는 99.9%가 되기 때문이다.
- 비율 불균형이 그리 크지 않더라도 정확도는 오해의 소지가 매우 크다. 잘못된 해석이 도출될 수 있다.
- ex) cellular-churn problem
- 1000명의 churn 예측 모델을 A와 B가 각각 만들었다고 하자.

- A모델은 churn 클래스는 100% 예측하고, not churn 클래스는 60% 예측한다.
- B모델은 churn은 60%, not churn은 100% 예측한다.
- 이 경우 두 모델은 매우 다르게 작동하지만 accuracy는 80%로 똑같다.
2) 또한, accuracy는 테스트 셋에 따라 달라진다.

3) false positive와 false negative를 구별하지 않는다.
- 둘을 같이 세기 때문에 오차들이 모두 똑같이 중요한 것처럼 여겨진다.
- 하지만, 이는 현실 세계에서는 드문 경우이다.
- 다른 종류의 오차는 다른 무게를 갖는다.
- ex) 의학 진단 경우
- false positive : 실제로 병에 걸리지 않았지만 걸렸다고 진단한 경우 (기분은 나쁠 수 있지만 실제로 정상이기 때문에 괜찮음)
- false negative : 실제로 병에 걸렸지만 걸리지 않았다고 진단한 경우 (대처를 못하기 때문에 훨씬 심각한 문제를 초래함)
- ex) cellular-churn
- false positive : 떠날거라고 생각해서 상품을 제공했지만 떠나지 않음 (어쨌든 고객을 유지했기 때문에 괜찮음)
- false negative : 떠나지 않을거라고 생각해서 제공하지 않았지만 떠남 (고객을 잃었기 때문에 훨씬 손해임)
- 대부분의 경우, 우리는 false positive와 false negative를 다르게 다뤄야 한다.
- classifier에 의한 각 결정들의 cost나 benefit을 추정해야 한다.
- 일단 집계되면, 이러한 것들은 classifier에 대한 기대이익(or 기대비용) 추정치를 산출할 것이다.
2-3. Generalizing beyond classification
- 데이터사이언스를 활용할 때 목표가 무엇인지, 주어진 목표에 맞게 데이터마이닝 결과를 적절히 평가하고 있는지 중요하게 생각해야 한다.
- ex) Regression
- 데이터사이언스팀이 영화 추천 모델을 만든다고 생각해보자.
- 평점은 1 - 5개의 별을 줄 수 있고, 모델은 사용자가 보지 않은 영화를 얼마나 많이 시작할지 예측한다.
- 모델을 오차의 평균으로 측정해야 할까, 오차 제곱의 평균으로 측정해야 할까?
- 더 나은 방법이 있는지 확인해야 한다.

3. Expected Value (EV) : Key Framework
- EV는 데이터 분석적 사고를 돕는 아주 유용한 개념적 도구이다.
- 데이터 분석 문제에 대한 생각을 정리하는데에 아주 유용한 핵심 프레임워크를 제공한다.
- 다음은 EV의 일반적인 계산식이다.

- o𝑖 : 가능한 결정 결과 (ex: classification -> YES or NO)
- p(o𝑖) : o𝑖의 확률
- v(o𝑖): o𝑖의 가치 (ex: cost, benefit or profit)
3-1. Using EV for Classifier Use (ex. 타겟 마케팅)
- 각 소비자의 클래스를 예측하여 더 응답할 가능성이 높은 고객들을 예측하고자 한다.
- 불행히도 타겟 마케팅의 경우 각 소비자가 응답할 확률은 대부분 1-2%로 매우 낮다.
- 그래서 우리가 상식적으로 응답할만한 소비자를 결정하기 위해 임계값을 50%로 정한다면 아마 아무도 겨냥하지 못할 것이다.
- 아마 모든 소비자가 '응답하지 않을 것'이라고 분류될 것이기 때문이다.
- 하지만, EV 프레임워크를 활용하면 문제의 핵심을 찾을 수 있을 것이다.
- feature vector가 x인 고객들에게 pᵣ(x)를 부여하는 모델을 갖고 있다고 가정하자.
- pᵣ(x)는 고객 x가 응답할 확률의 추정치이다.
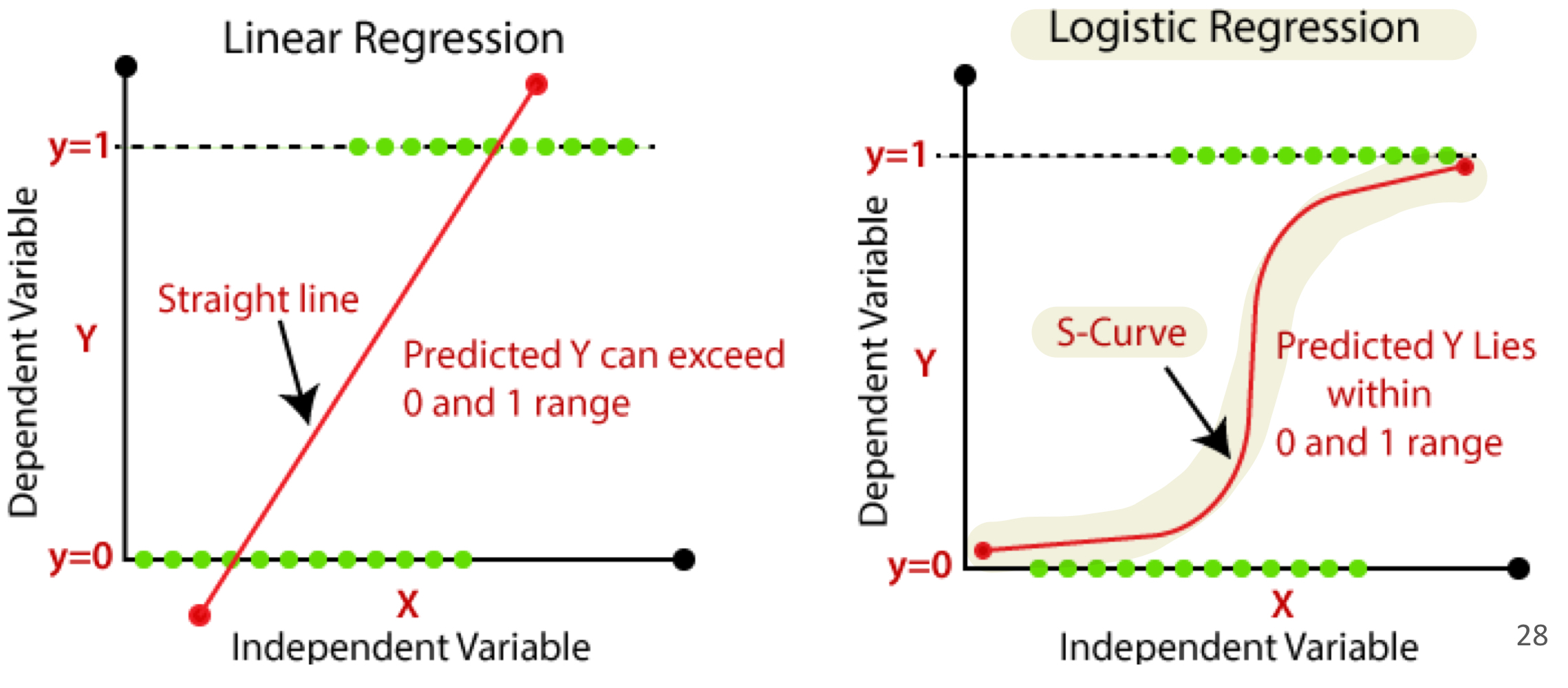
- 예를 들면 classification tree, logistic regression model 등이 있다.
- 그러면 이제 다음과 같이 타겟 고객 x의 기대 수익 (or 기대 비용)을 계산할 수 있다.

- vᵣ : 우리가 응답으로부터 얻는 가치 (value from a response -> profit)
- vₙᵣ : 무응답으로부터 얻는 가치 (value from no response -> cost)
- example scenario
- 상품가격 $200
- 원가 $100
- 마케팅비 $1
- EV 계산식에서 vᵣ = $99, vₙᵣ = -$1
- 우리는 EV가 0보다 크기만 해도 이익을 얻는 것이다.
따라서 계산을 해보면 pᵣ(x) · $99 - (1 - pᵣ(x)) · $1 > 0
=> pᵣ(x) > 0.01
- 고객 x가 응답할 확률이 1%만 돼도 남는 장사라는 것을 알 수 있다.
- 따라서 우리가 예상했던 50% 응답률이 아니라, 1% 보다 큰 확률 추정치를 갖는 고객을 타겟으로 삼아야 한다.
3-2. Using EV for Classifier Evaluation
- 지금까지 개개인의 결정에 주목했다면, 지금부터는 '결정의 집합'에 더욱 주목하고자 한다.
- 특히 우리는 모델로부터 만들어진 일련의 결정들을 평가해야 한다.
- 이 평가를 할 때 서로 다른 모델들을 비교하는 것이 필요하다.
- 우리의 데이터 중심 모델은 직접 만든 모델보다 더 성능이 좋은가?
- 분류 트리 모델이 로지스틱 회귀 모델보다 더 성능이 좋은가?
- 총체적으로 우리가 관심을 가지는 것은 각 모델이 얼마나 잘 수행하는지, 즉 그것의 expected value가 무엇인지이다.
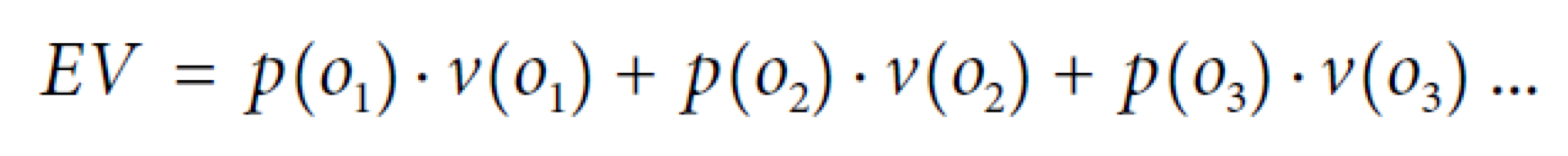
- EV의 일반 계산식이다.
- 각 o𝑖는 예측 클래스와 실제 클래스의 가능한 조합 중 하나에 해당한다.
((Y,p),(Y, n), (N, p). (N, n))
- 그리고 p(o𝑖)는 이미 confusion matrix에 나와있다.

- 각 o𝑖는 confusion matrix의 각 셀에 해당한다.
- ex)
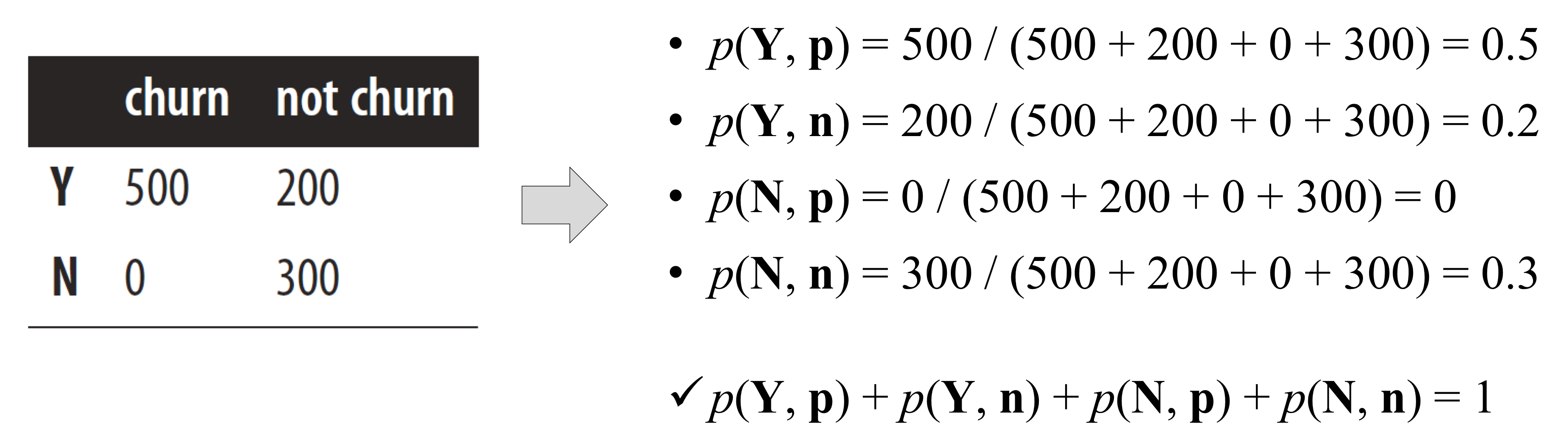
1) step 1 : 각 케이스의 비율을 측정한다. (p(o𝑖))
- 각각의 count를 총 개체 수로 나눈다.
- p(h, a) = count(h, a) / T
- h : 예측된 클래스 (Y / N)
- a : 실제 클래스 (p / n)
- T : 총 개체 수
- count(h, a) : (h, a)케이스에 해당하는 개체 수
- p(h, a) : (h, a)케이스의 비율 (or 확률 추정치)

2) step 2 : 각 케이스의 value를 명시한다. (v(o𝑖))
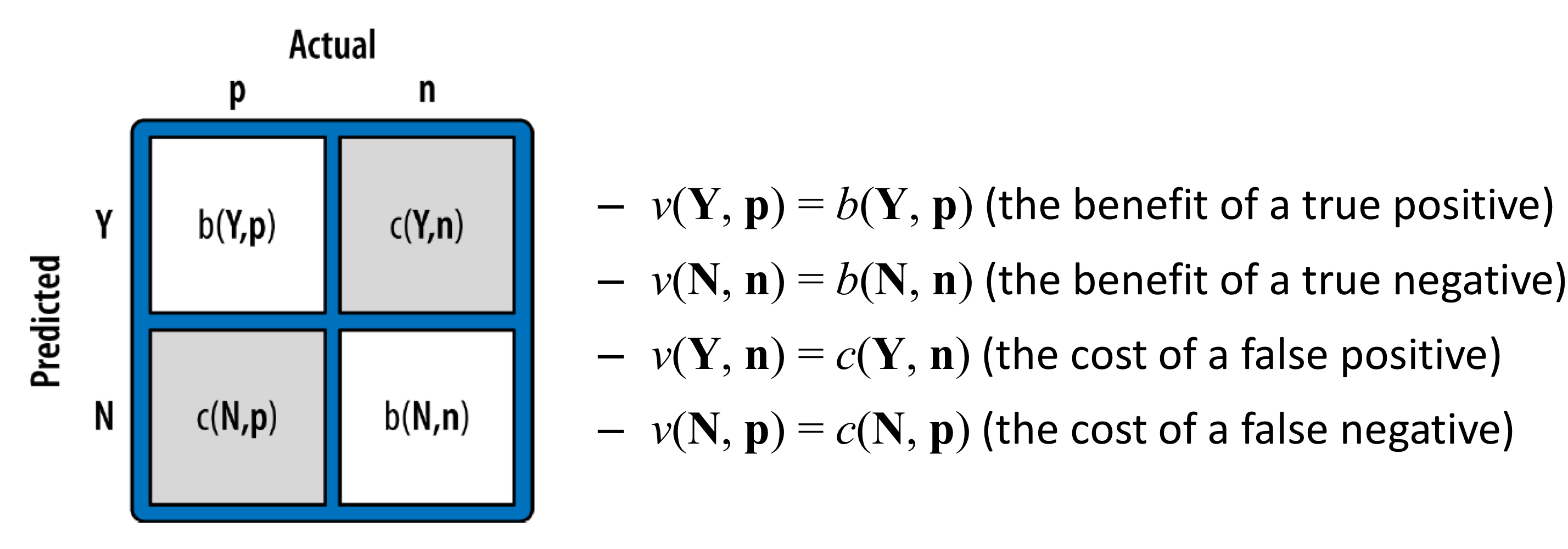
- 하지만, b(h, a)와 c(h, a)는 데이터로부터 추정할 수 없다.
- 이 둘은 일반적으로 분석으로부터 제공되는 외부 정보에 의해 정해진다.
- 그것들을 지정하는 것은 많은 시간과 노력이 필요하다. (ex: 우리가 고객을 유지하는 것이 정말 어느정도의 가치가 있는가?)
- ex) 위의 example scenario 예제
- v(Y, n) = -1
- v(N, p) = 0
- p(Y, p) = 99
- p(N, n) = 0
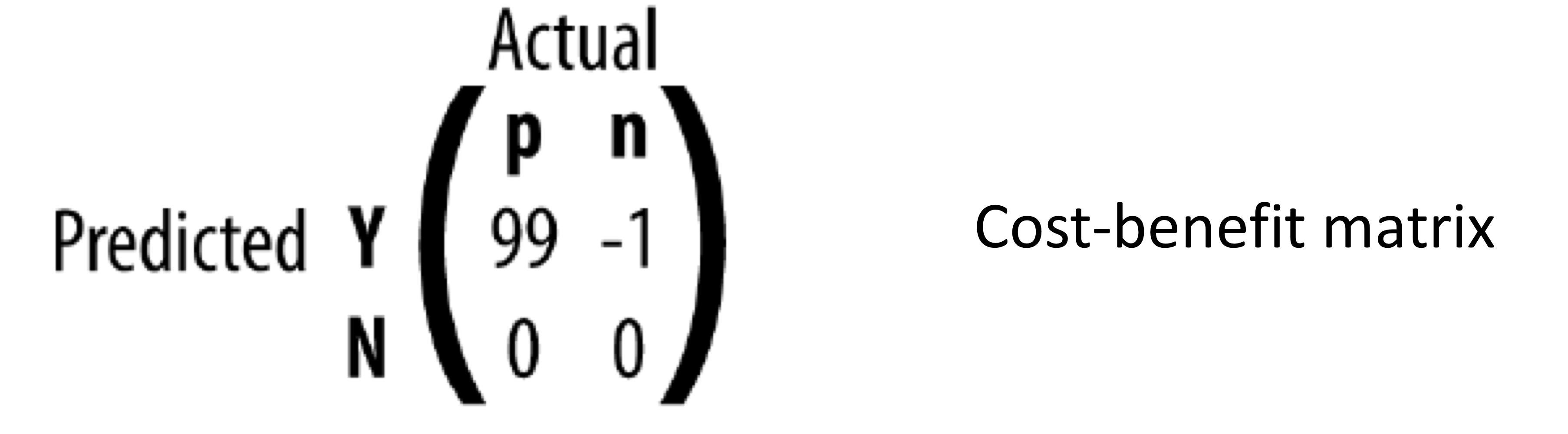
3) step 3 : total expected value (or profit) 을 계산한다.
- 다음 공식을 통해서 모델의 expected profit을 계산한다.
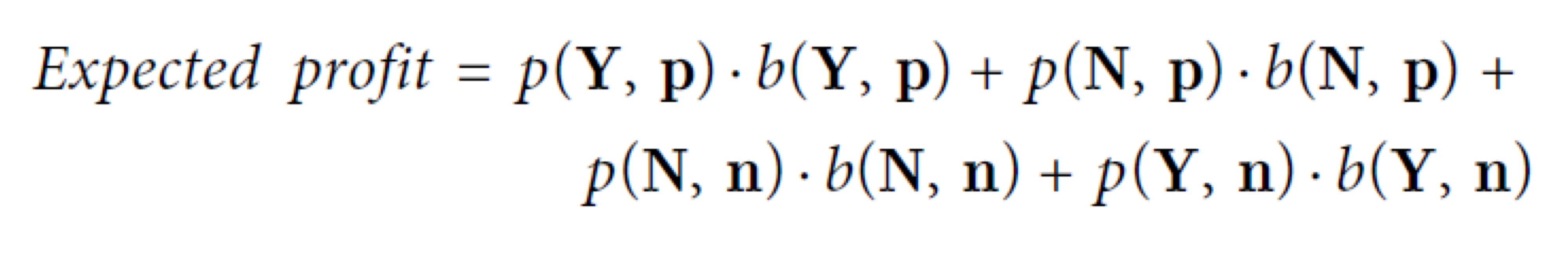
- final value는 각 고객 당 total expected profit을 나타낸다.
- 따라서 우리가 필요한 것은
- 테스트 데이터셋에 대한 confusion matrix 계산
- p(Y, p), p(Y, n), p(N, p), p(N, n)
- cost-benefit matrix 생성
- v(Y, p), v(Y, n), v(N, p), v(N, n)
3-3. Alternative Calculation of EV
- alternative calculation은 종종 실제로! 사용되는 것이다.
- 왜냐하면 우리가 모델 비교 문제를 어떻게 다뤄야 하는지 정확히 알 수 있기 때문이다.
- 조건부확률
- 사전 class : p(p) and p(n)
- 각각 positive와 negative 개체일 확률이다.
- p(x, y) = p(y) · p(x | y)
- p(x | y) = p(x, y) / p(y)
- (p(x, y) : x 와 y의 교집합)
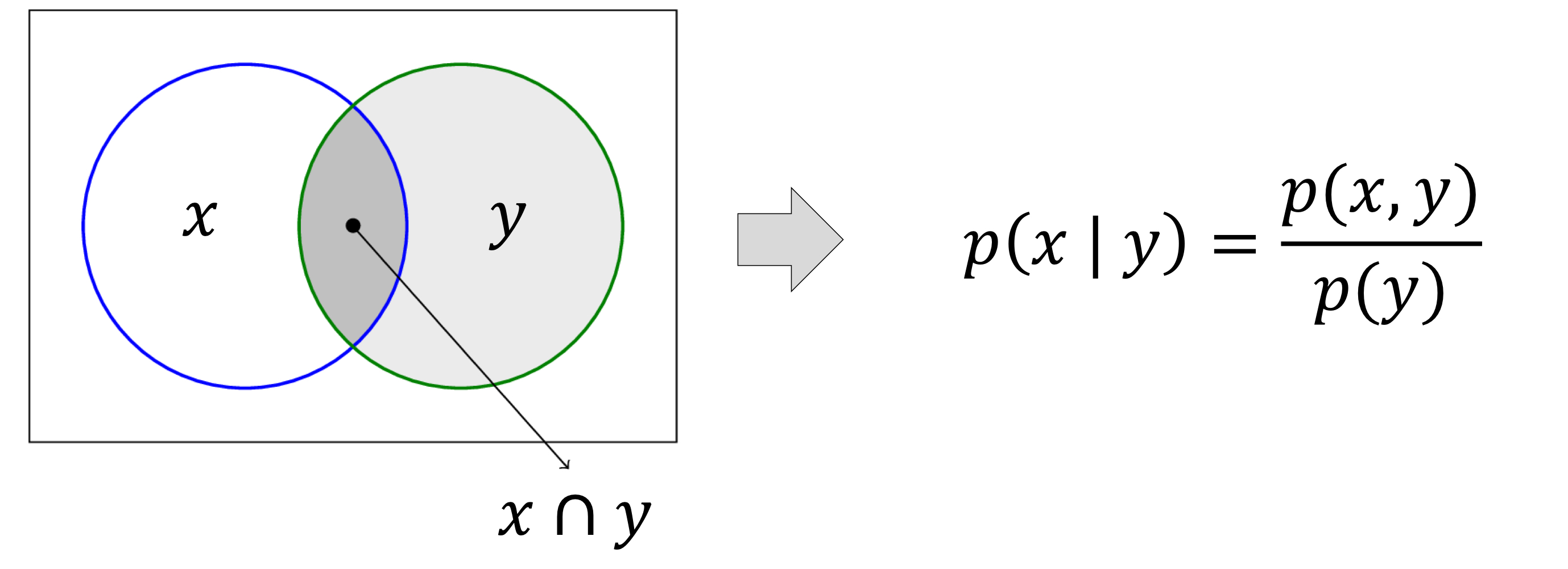
- 다음과 같이 사전 클래스 p(p)와 p(n)을 찾아낼 수 있다.

- ex)

- expected profit = p(p) · [p(Y | p) · b(Y , p) + p(N | p) · b(Y , p)] + p(n) · [p(Y | n) · b(Y, n) + p(N | n) · b(N, n)]
= 0.55 (0.92 · 99 + 0.08 · 0) + 0.45 (0.14 · -1 + 0.86 · 0)
≈ $50.04
- 이를 통해 각 고객 당 평균적으로 약 $50 의 이익을 얻을 수 있다고 예측할 수 있다.
- 이제 경쟁 모델에 대한 정확도를 계산하는 대신에, expected values를 계산할 것이다.
- 나아가, 다양한 분포에 대해 두 모델을 쉽게 비교할 수 있다.
- 각 분포에 대해 우리는 쉽게 사전확률을 대체할 수 있다.
- 예를 들어, 불균형한 분포는 p(p) = 0.7, p(n) = 0.3 // 균등한 분포는 p(p) = 0.5, p(n) = 0.5라고 할 수 있다.
- expected profit = p(p) · [p(Y | p) · b(Y , p) + p(N | p) · b(Y , p)] + p(n) · [p(Y | n) · b(Y, n) + p(N | n) · b(N, n)] 에서
p와 n의 분포가 아무리 바뀌어도 [ ] 속에 있는 비율들은 변하지 않기 때문에 p(p)와 p(n)의 값만 바꾸어서 계산하면 된다.
- p(p), p(n)을 제외한 다른 비율들이 변하지 않는 이유는 같은 모델이기 때문이다.
4. Overview of the EV Calculation

5. Other Evaluation Metrics
- 데이터 사이언스에 사용되는 많은 평가 지표들이 있다.
- 모든 지표들은 근본적으로 confusion matrix의 요약본이다.
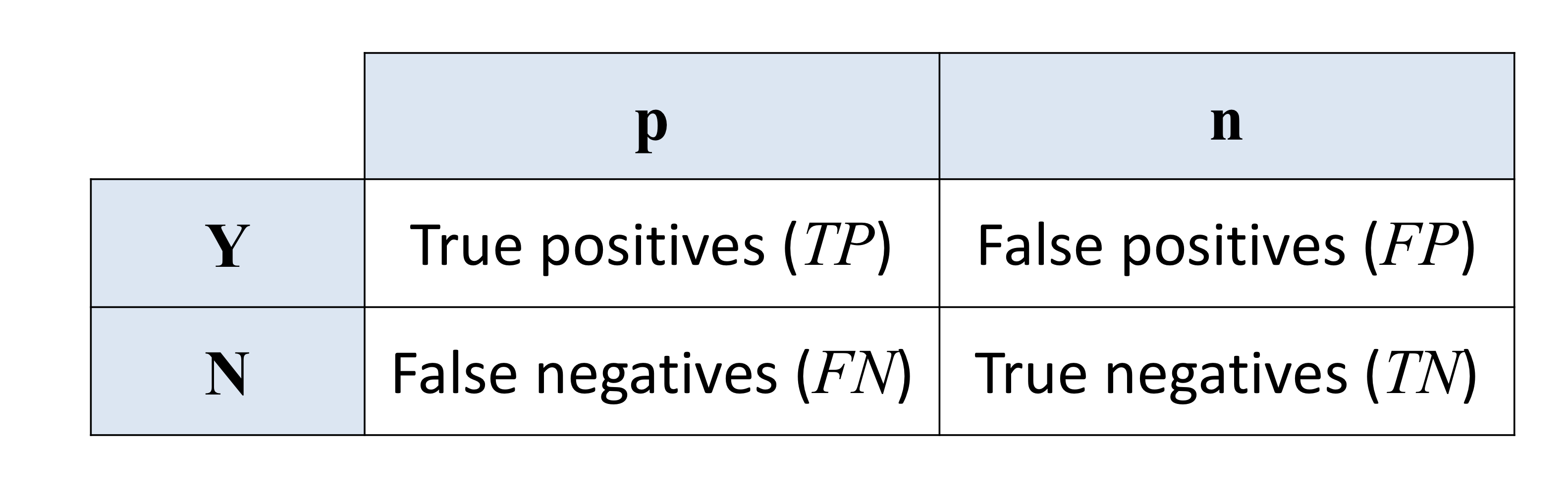
- Accuracy = (TP + TN) / (TP + FN + FP + TN) : 전체 개체 중 맞은 예측의 비율
- True positive rate (=Sensitivity) = TP / (TP + FN) = 1 - False negative rate : positive 중 맞춘 예측의 비율
- False negative rate = FN / (TP + FN) : positive 중 틀린 예측의 비율
- True negative rate (=Specificity) = TN / (FP + TN) = 1 - False positive rate : negative 중 맞춘 예측의 비율
- False positive rate = FP / (FP + TN) : negative 중 틀린 예측의 비율
- Precision 정밀도 = TP / (TP + FP) : positive 로 예측한 경우에서의 정확도
- Recall 재현율 = TP / (TP + FN) =True positivve rate (Sensitivity)
- F-measure F-값 = 2 x {(Precision x Recall) / (Precision + Recall)} : precision과 recall의 조화평균
- 이 세 가지는 정보 검색과 패턴 인식 (텍스트 분류) 에 널리 사용된다.
6. Baseline Performance
- 몇몇 경우, 우리는 모델이 어떤 기준선보다 더 나은 성능을 갖고있다고 증명해야 한다.
- 그렇다면 비교의 대상이 되는 적절한 기준선은 무엇일까?
- 그것은 실제 용도에 따라 다르다.
- 하지만 몇몇 일반적인 원칙들이 있다.

1) Random model
- 통제하기 쉬울 수 있지만, 그다지 흥미롭거나 유익하진 않을 것이다.
- 매우 어려운 문제나 처음 문제를 탐색할 때 유용할 것이다.
2) Simple (but not simplistic) model
- ex) weather forecasting
- 내일의 날씨는 오늘과 같을 것이다.
- 내일의 날씨는 과거부터 내일까지의 날씨의 평균일 것이다.
- 각 모델은 랜덤으로 예측하는 것보다 훨씬 나은 성능을 발휘한다. 어떤 새롭고 더욱 복잡한 모델도 이것들보다는 나은 성능을 가져야 한다.
3) The majority classifier 다수결
- 항상 훈련 데이터셋에서 다수의 클래스를 선택하는 방법이다.
- 우리는 모집단의 평균 값이라는 직접적으로 유사한 기준선을 가지고 있다.
- 보통 평균이나 중간값을 사용한다.
- ex) 추천 시스템 - 특정 영화가 주어졌을 때 고객이 몇개의 별점을 줄 지 예측해보자. - random model - simple models - model 1 : 고객이 영화들에게 준 별점의 평균 값을 사용할 것이다. - model 2 : 대중이 그 영화에 준 별점의 평균 값을 사용할 것이다. - combination of multiple simple models : 이 둘에 기초한 간단한 예측은 둘 중 하나를 따로 사용하는 것보다 훨씬 낫다.
- 간단한 모델을 비교하는 것 외에도, 배경 지식을 기반으로 한 간단하고 저렴한 모델을 기본 모델로 사용할 수 있다.
- ex) Fraud detection 사기 탐지 - 일반적으로 대부분 사기당한 계정들은 갑자기 사용률이 늘어난다고 알려져 있다. - 거래량 급상승에 대한 계좌 조회는 많은 사기를 잡기에 충분했다. - 이 아이디어를 구현하는 것은 간단하며, 유용한 기준선을 제공했다.
'Software > Data Science Introduction' 카테고리의 다른 글
| [데이터사이언스개론] Evidence and Probabilities (0) | 2021.06.09 |
|---|---|
| [데이터사이언스개론] Visualizing Model Performance (0) | 2021.06.09 |
| [데이터사이언스개론] Similarity, Neighbors, Clusters (0) | 2021.06.04 |
| [데이터사이언스개론] Overfitting and Avoidance (0) | 2021.04.22 |
| [데이터사이언스개론] Fitting Model to data (0) | 2021.04.22 |