수업출처) 숙명여자대학교 통계학과 '통계수학' 수업, 윤재은 교수님
1. 역행렬
: 정방행렬 A 에 대해서 AB = BA = I 를 만족하는 정방행렬 B, A⁻¹로 표시
역행렬이 존재하기 위한 조건은 A가 정방행렬이면서 det(A) ≠ 0이어야 한다.
* 2차 정방행렬 역행렬 구하는 방법
A = [a b; c d]
|A| = ad - bc
A⁻¹ = 1 / (ad - bc) [d -b; -c a]
2. 역행렬 성질
Th3.1 > 정방행렬 A의 역행렬이 존재하는 경우 그 역행렬은 유일하다.
Th3.2 > A의 역행렬이 존재하기 위한 필요충분조건은 |A| ≠ 0이다.
Th3.3 > A가 가역행렬이면 A⁻¹ 역시 가역이며 (A⁻¹)⁻¹ = A 이다.
** 가역 = 정칙 = 역행렬 존재
Th3.4 > (A⁻¹)T = (AT)⁻¹
Th3.5 > A와 B가 각각 정칙이면 AB 역시 정칙이며 다음이 성립한다.
> (AB)⁻¹ = B⁻¹ A⁻¹
> (ABC)⁻¹ = C⁻¹ B⁻¹ A⁻¹
Th3.6
> A가 가역행렬일 때 kA도 가역행렬이고 (kA)⁻¹ = 1/k A⁻¹ 이다.
> A가 가역행렬일 때 Aⁿ 도 가역행렬이고, (Aⁿ)⁻¹ = (A⁻¹)ⁿ 이다.
Th3.7> A가 정칙일 때, PA = QA 이면 P = Q 이다.
Th3.8 > Ax = b 에서 A가 정칙이면 x = A⁻¹ b 이다.
→ 연립방정식의 풀이에 활용할 수 있음
3. 행렬의 분할
: 행렬을 블록화하여 간단히 나타낼 수 있다.
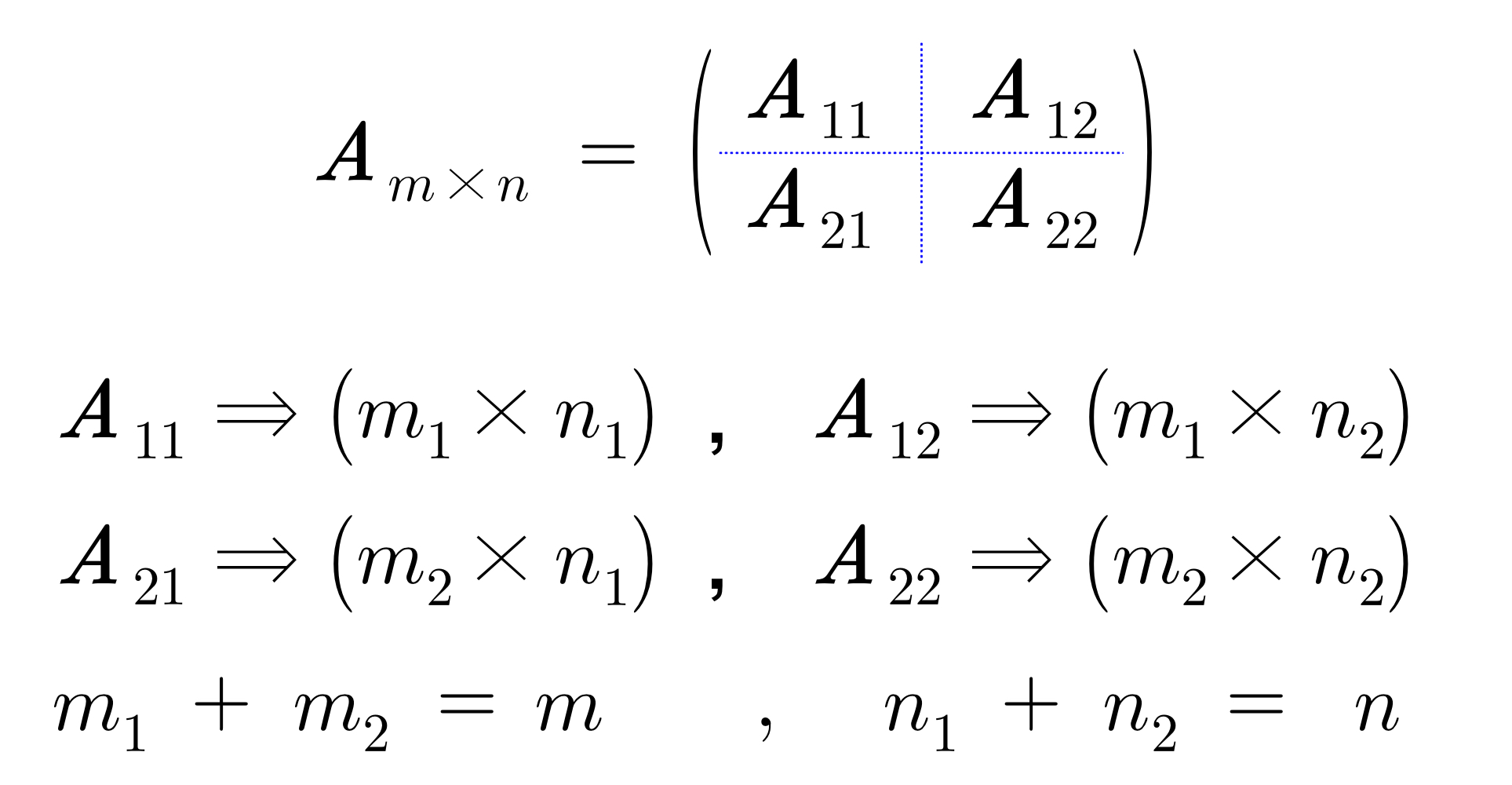
* 분할행렬의 전치행렬은 각각의 분할된 행렬을 전치한 것과 같다.
* 분할행렬의 곱

'Statistics > 통계수학' 카테고리의 다른 글
| [행렬] 행렬의 rank (0) | 2021.04.24 |
|---|---|
| [행렬] 직교성과 정사영 (0) | 2021.04.24 |
| [행렬] 벡터의 선형독립과 내적 (0) | 2021.04.24 |
| [행렬] 행렬식 (0) | 2021.04.13 |
| [행렬] 행렬의 기초 (0) | 2021.04.13 |