gnuykob_sw

수업 출처) 숙명여자대학교 소프트웨어학부 박동철 교수님 '데이터사이언스개론' 수업

1. Evidence-Based Classification 

- 지금까지 분류를 위한 여러 방법을 알아보았다.

- 이제 분류의 다른 방법을 알아볼 것이다.

- Evidence 

    - 실제 일어난 것들. 실제 data 값들. (data instance의 feature values)

    - data의 각각의 feature vector를 타겟 값에 대한 증거 (evidence)로 생각할 수 있다.

- 각 feature에 의해 주어진 증거의 강점을 안다면, 그것들을 확률적으로 결합하여 개체를 분류할 수 있다.

- 훈련 데이터로부터 각 증거의 강도를 알 수 있다.

2. (ex) online targeting advertising

- 고객들이 과거에 방문한 웹페이지를 기반으로 온라인 타겟 광고를 한다고 생각해보자.

- 웹페이지의 상단, 사이드, 하단에 광고를 띄우려고 한다.

- 화면 광고의 특징

    - 검색 결과를 바탕으로 나타나는 검색 광고와는 다르다. 

    - 사용자들은 어느 키워드도 입력하지 않는다.

    - 그러므로 우리는 사용자의 feature values를 기반으로 사용자가 특정 광고에 관심이 있는지 없는지 유추할 필요가 있다.

- 광고 타겟팅 문제를 더욱 정확하게 정의내려보자.

- 네이버나 페이스북과 같은 매우 큰 컨텐츠 제공자와 일하고 있다고 가정해보자.

    - 다양한 컨텐츠, 많은 온라인 고객들을 보유하고 있다.

- 우리 웹사이트를 방문하는 고객들의 몇몇 부분집합을 타겟으로 하고자 한다.

- 이 광고 캠페인은 호텔을 광고하기 위해서 진행된다. 사람들이 호텔 방을 예약하도록 하는 것이 목표이다.

- 훈련 데이터를 얻기 위해서 우리는 온라인 고객들을 랜덤으로 선택하여 이 캠페인을 과거에 진행했다.

- 이제 우리가 원하는 것은 '타겟 고객을 대상으로' 광고 캠페인을 진행하는 것이다.

- 그를 통해 광고에 사용하는 비용 대비 많은 예약자를 얻고자 하는 것이다.

- 광고 타겟팅 문제를 어떻게 정의할 수 있을까?

    - instance는 무엇이 될까

    - 타겟 변수는 무엇이 될까

    - 특성들은 무엇이 될까

    - 훈련 데이터는 얼마나 모아야 할까

    - 어떤 분류 모델을 이용해야 할까

- 다음과 같이 정의하고자 한다.

    - instance : 고객

    - target variable : 그 고객이 이 호텔 광고를 본 뒤 일주일 내에 예약을 한 적이 있거나 할 예정인가?

    - features : key question! 이후에 다룰 예정

    - training data : 타겟 변수에 대한 이진값 (Y / N)

    - classification model : 광고를 본 후 방을 예약할 고객의 확률을 추정하기 위해 Naive Bayes classifier을 사용할 것이다.

- key question) 고객을 묘사하기 위해 어떤 특징 (features)을 활용해야 할까?

    - 어떤 attribute가 필요할까

    - 호텔에게 좋은 고객이 될 가능성이 높은 고객과 낮은 고객들을 차별화할 수 있도록 해야 한다.

- 이 예제에서 (호텔)는 고객이 이전에 방문했던, 혹은 좋아요를 눌렀던 컨텐츠들의 집합을 feature로 활용할 것이다.

    - ex) Jessie = {www.sookmyung.ac.kr, "Avengers: Endgame", ...}

    - 브라우저 쿠키나 다른 메커니즘을 통해 기록된 것을 이용할 것이다.

- 각 증거(컨텐츠 조각들)의 강도와 방향을 추정하기 위해 과거 데이터를 활용할 것이다.

    - 그리고 클래스 멤버십의 가능성을 추정하기 위해 그것들을 결합할 것이다.

- 이 예제의 framework와 잘 맞는 여러 다른 문제들이 있다.

    - 각 개체는 증거들의 집합으로 묘사된다.

    - 우리는 개체를 분류하기 위해서 각 증거 조각의 강도를 결합해야 한다.

- ex) spam detection

    - 각 메일은 단어들의 집합으로 구성되어 있다.

    - 각 단어들이 이 메일이 스팸인지 아닌지 구분하는 증거가 된다.

    - 메일을 분류하기 위해 증거들을 확률적으로 결합할 것이다.

    - problem definition

        - instance : an email message

        - target classes : spam or not-spam

        - features : the words (and symbols) in the email message

3. Combining Evidendce Probabilistically

- 우리는 고객이 광고를 본 후 호텔 룸을 예약할 확률을 알고싶다.

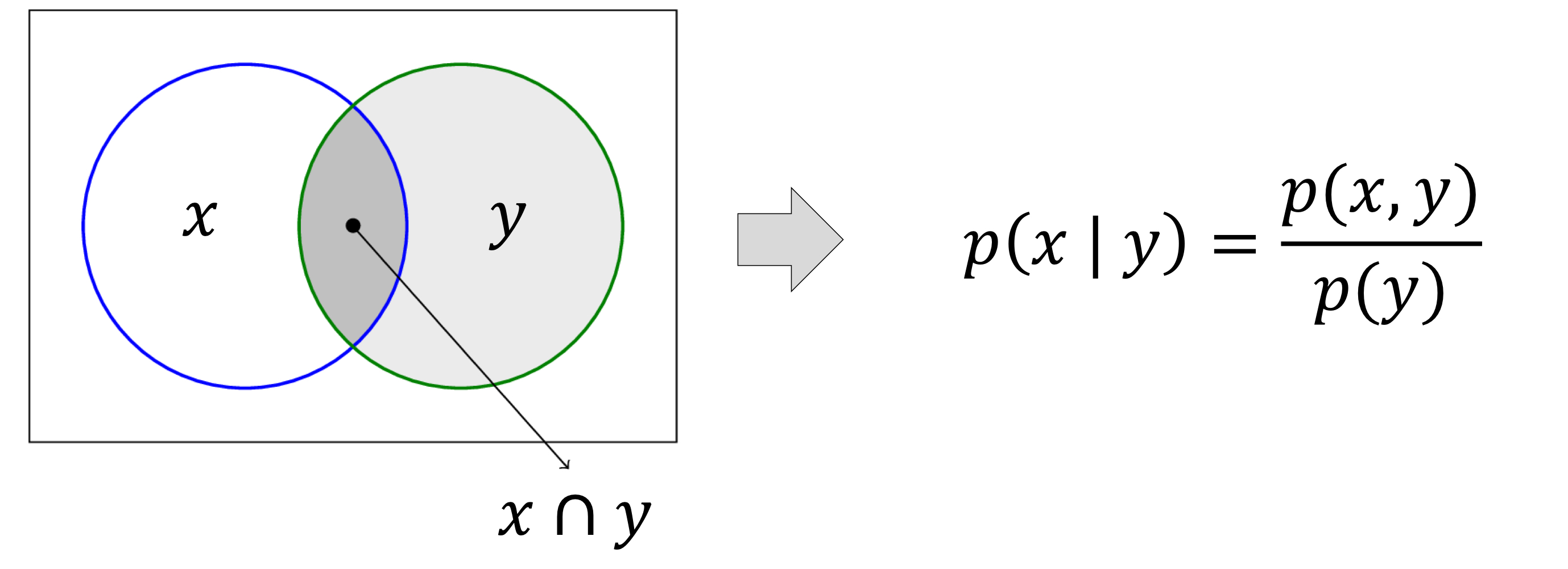
- 사건이 일어날 확률을 p(C)라고 하면, 우리는 조건부 확률인 p(C | E)에 관심을 가져야 한다.

    - E = {e1, e2, ..., ek} : 고객이 방문한 웹사이트들의 집합

    - C : 고객이 룸을 예약하는 사건

- E가 달라질 때마다 p(C | E)도 달라질 것이다. 즉, 서로 다른 웹사이트를 방문한 고객들은 서로 다른 행동을 보일 것이다.

- 훈련 데이터를 통해서 p(C | E)를 유추할 수 있다.

- 하지만, 중요한 문제가 있다. 훈련 데이터에서 정확히 똑같은 집합의 증거를 가진 개체 (k개의 웹사이트를 똑같이 방문한 사람) 는 거의 없을 것이다. 

- 따라서 증거를 하나씩 분리해서 고려한 후에 다시 합쳐야 한다.

- 즉, E = {e1, e2, ..., ek} 일 때, e1, e2, ..., ek를 각자 분리해서 계산한다는 뜻이다.

4. Joint Probability

- Notations

    - A, B : 두 사건

    - p(A), p(B) : A와 B가 각각 일어날 확률

    - p(AB) : 두 사건이 동시에 일어날 확률 -> joint probability

- 두 사건 A, B가 독립인 경우 p(AB) = p(A) · p(B)

- 독립이 아닌 경우 p(AB) = p(A) · p(B | A)

5. Bayes' Rule 

- p(AB) = p(A) · p(B | A) = p(B) · P(A | B)

==> p(B | A) = {p(A | B) · p(B)} / p(A)

- A와 B를 각각 E, H라고 하자.

- H : 가능성을 평가하고자 하는 어떠한 가설

- E : 우리가 관찰할 수 있는 증거

==> p(H | E) = {p(E | H) · p(H)} / p(E)

- 이것이 베이즈 정리이다.

- p(H | E)를 구할 때 p(E | H)를 대신 살펴봄으로써 증거 E가 주어졌을 때 가설 H의 확률을 계산할 수 있다.

- 즉, p(E | H), p(H), p(E)를 통해서 p(H | E)를 구할 수 있다는 장점이 있다.

6. Importance of Bayes' Rule

- p(E | H), p(H), p(E)가 p(H | E)보다 결정하기 쉽다.

- ex) medical diagnosis

    - 예를 들어, 내가 의사이고 빨간 반점을 가진 환자가 찾아왔다고 가정해보자.

    - 나는 환자가 홍역을 갖고 있다고 추측할 수 있다.

    - H를 '홍역', E를 '붉은 반점'이라고 할 때, p(H | E)를 구해야 한다.

    - 하지만 p(H | E)를 바로 구하는 것은 거의 불가능하다.  

    - 왜냐하면 그 확률을 구하려면 한 사람에게 붉은 반점이 나타날 수 있는 모든 사례들과 그 중 홍역일 비율을 생각해야 하기 때문이다.

    - 하지만, 대신 p(E | H), p(H), p(E)를 구해본다면,

    - p(E | H) : 홍역일 때 붉은 반점이 생길 확률

    - p(H) : 어떤 사람이 홍역에 걸릴 확률

    - p(E) : 어떤 사람에게 붉은 반점이 생길 확률

    - 이 확률들은 전문가로부터 이미 알려져 있거나 직접 구할 수 있다.

    - 따라서 베이즈 정리를 통해서 p(H | E)를 더욱 쉽게 구할 수 있다.

7. Applying Bayes' Rule to Classification

- 데이터 사이언스의 많은 부분이 베이지안 방법에 기반을 두고 있다.

- 그들의 핵심 논리가 베이지 정리에 근거한 것이다. 

- p(C = c | E) = {p(E | C = c) · p(C = c)} / p(E)

    - C = c : 타겟 변수값이 c인 사건 (ex: C = 'YES' or C = 'NO')

    - E : 증거 (the vector of feature values)

    - p(C = c | E) : 증거가 E일 때 C = c일 확률. 우리가 구하고 싶은 값이며 '사후확률 (posterior probability)'라고 부른다.

    - p(C = c) : 클래스 c의 사전확률. 모든 예시들 중 class가 c일 확률

    - p(E | C = c) : 클래스 C = c일 때 증거가 E일 확률. feature vector가 E인 클래스 c의 비율

    - p(E) : E일 가능성. 모든 예시들 중 E가 발생할 확률

    - 아래 세 가지 확률은 데이터로부터 쉽게 구할 수 있다.

- 사후확률 p(C = c | E)

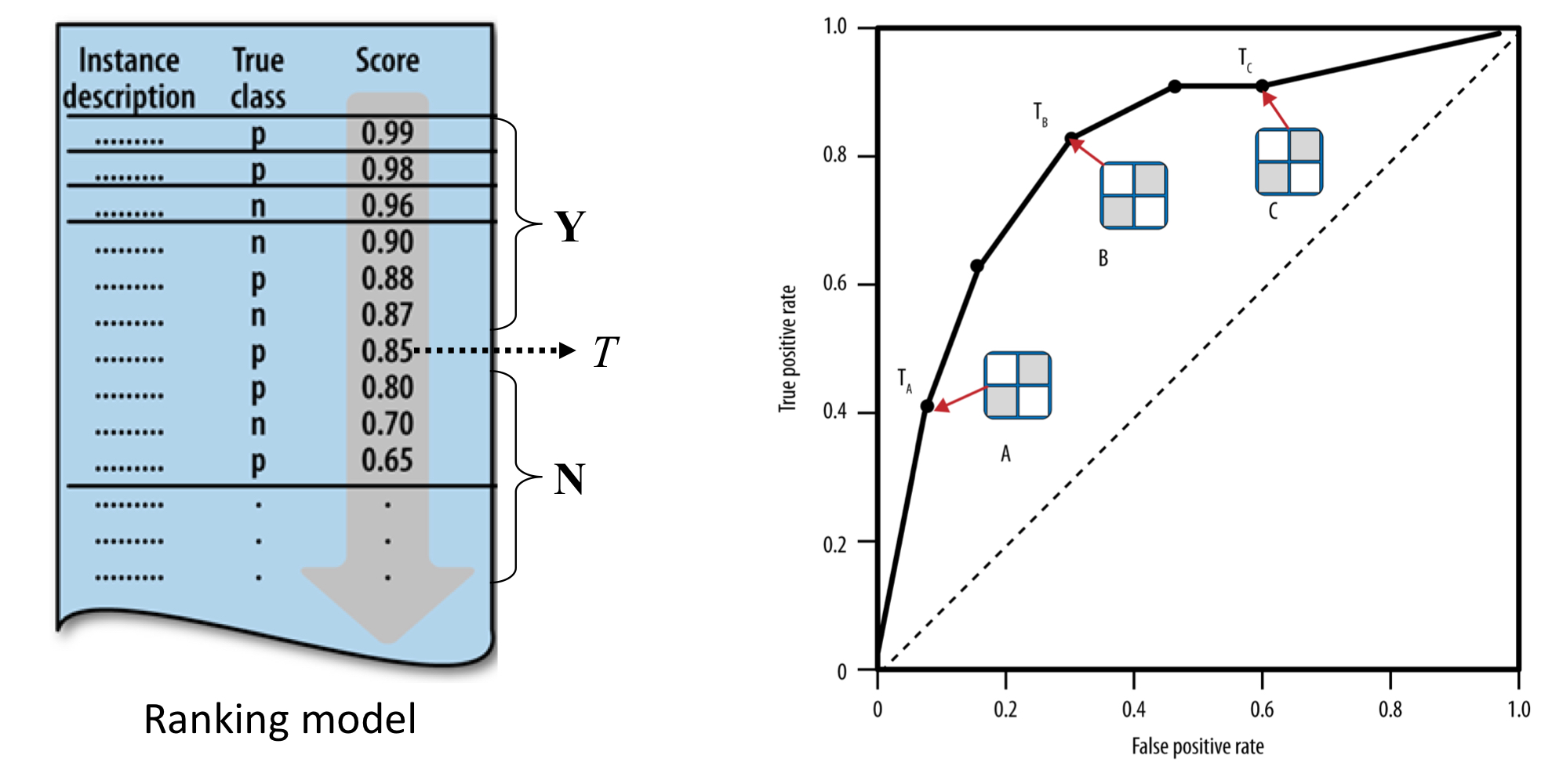
    - 클래스 확률의 추정치로 바로 사용할 수 있다.

    - 개체들의 순위를 매기기 위한 점수로 사용할 수 있다.

    - 또는, 분류할 때 서로 다른 c값에 대해 p(C = c | E)의 최댓값을 선택할 수 있다.

    - ex) p(C = 'YES' | E) = 0.7, p(C = 'NO' | E) = 0.3 -> determine C = 'YES'

- ex) spam detection

    - w1, ..., wn : 메일 속 단어들

    - p(Spam | w1, ..., wn) = {p(w1, ..., wn | Spam) · p(Spam)} / p(w1, ..., wn)

8. Major Difficulty in Computing p(C = c | E)

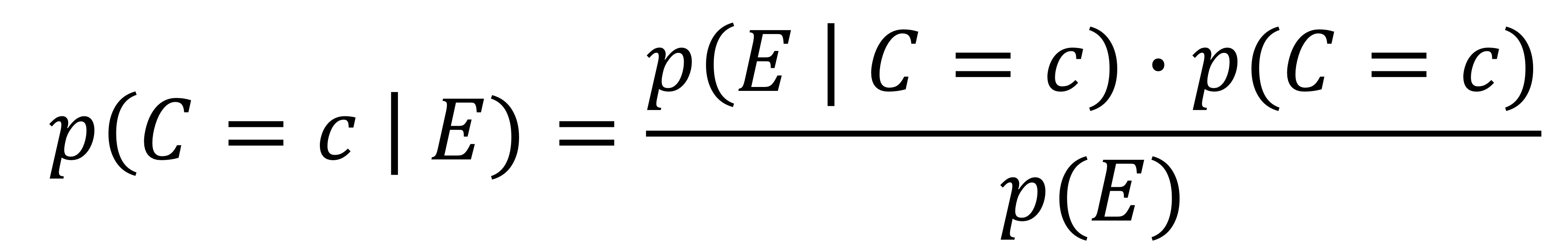
- E = {e1, e2, ..., ek}

- E는 충분히 크고, 구체적인 조건들의 집합이다.

- p(E | C = c) = p(e1, e2, ..., ek | C = c)

- 하지만 p(e1, e2, ..., ek | C = c)를 구하는 것은 어렵다. 

- 훈련 데이터에서 증거가 주어진 E  = {e1, e2, ..., ek}와 완전히 일치하는 특정 개체를 절대 볼 수 없을지도 모른다. 

- 만약 존재한다고 하더라도 확신을 가지고 확률을 추정할만큼 충분히 있진 않을 것이다.

9. Conditional Independence

- p(AB | C) = p(A | C) · p(B | AC) = p(B | C) · p(A | BC)

- C가 일어날 때 A와 B는 독립적이지 않다.

- 하지만, C가 일어날 때 조건적으로 A와 B가 독립이라면

- p(AB | C) = p(A | C) · p(B | C) = p(B | C) · p(A | C)

- 이 경우가 더 확률을 계산하기 쉽다.

- 따라서 데이터사이언스의  베이지안 방법에서는 '조건부 독립'을 강하게 가정함으로써 이 문제를 다룬다.

- p(E | c) = p(e1 ^ e2 ^ ... ^ ek | C) = p(e1 | C) · p(e2 | C) · ... · p(ek | C)

- 클래스 c가 주어졌을 때, eᵢ를 다른 eⱼ와 독립적이라고 가정한다.

- 간단히 표현하기 위해서 C = c 를 c라고 표현하겠다.

- 각 p(eᵢ | c) 는 데이터로부터 바로 계산될 수 있다.

    - 모두 맞는 feature vector를 찾을 필요가 없다.

    - 단순히 클래스 c의 개체에서 각 feature eᵢ를 찾은 비율을 계산하면 된다.

    - 그러면 증거를 한 번에 비교하는 것보다 상대적으로 eᵢ가 많이 발생할 수 있다. 

10. Naive Bayes Classifier

- 이 전의 식과 베이즈 정리를 결합하면 다음과 같이 '나이브 베이즈 방정식 (Naive Bayes equation)'이 나온다.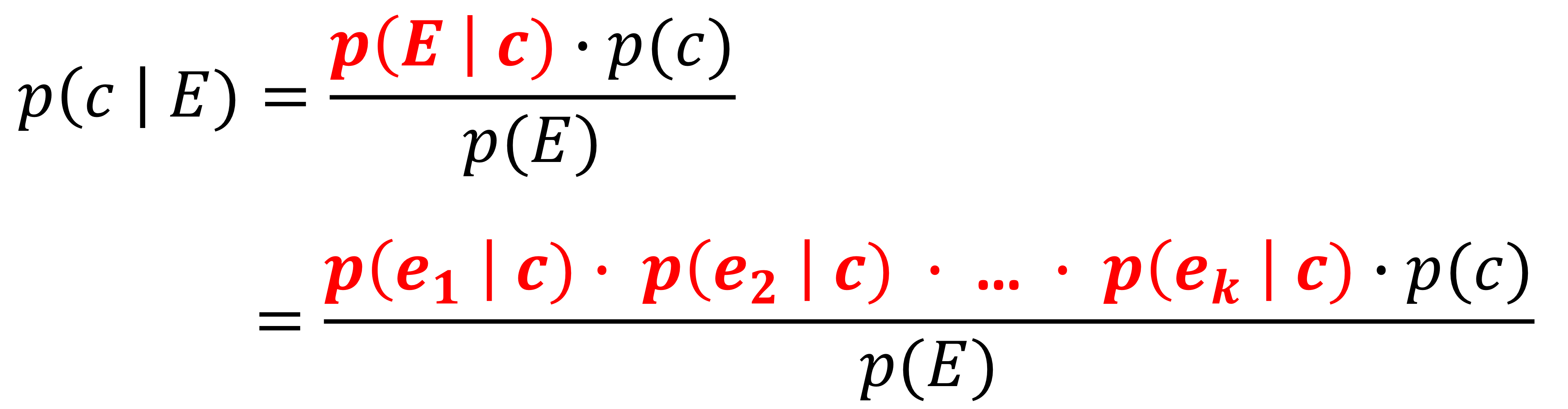 

- 베이즈 방정식을 활용하여 표본이 각 클래스에 속할 확률을 추정하는 방식이다.

- 더 높은 확률을 갖는 클래스를 반환한다.

- 예를 들어, Y에 속할 확률이 30%라고 치면, N에 속할 확률은 70%가 아니라 따로 또 계산을 해줘야 한다.

만약 N에 속할 확률이 45%라면 Y에 속할 확률보다 크기 때문에 N으로 분류한다.

- 우리는 분류에만 관심이 있기 때문에 정확한 값보다는 어떤 클래스에 속할 확률이 더 큰지가 더 중요하다.

- 따라서 실제로는 분모의 p(E)는 모든 클래스에 대해 똑같기 때문에 생략하고, 분자만 계산한다.

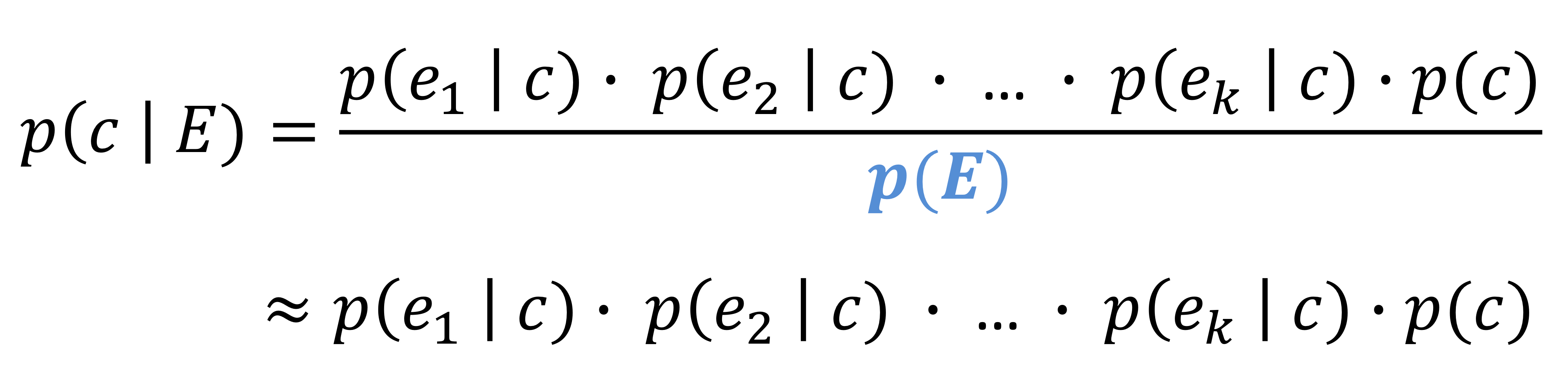
11. Advantage of Naive Bayes

- 매우 간단한 classifier이다. 

    - 그럼에도 불구하고 모든 특징 증거들을 고려한다.

- 저장공간과 실행시간에 대해 매우 효율적이다. 

    - 오직 p(c)와 p(eᵢ | c)만 저장하고, 몇몇의 간단한 곱셈만 수행하기 때문이다.

- 단순함과 강한 독립성 가정에도 불구하고 많은 실생활 문제들에서 놀라울 정도로 잘 수행된다.

    - 독립이 아닌 사건들에도 적용할 수 있다. 독립성 가정의 위반은 분류 성능을 낮추지 않는 경향이 있다.

    - 두 증거가 사실 독립적이지 않은데 독립적으로 다뤘다면 증거들의 double counting 문제가 생긴다.

    - (ex) p(AB) = p(A) · p(B | A) vs. p(AB) = p(A) · p(B)

    - 이는 classifier 측면에서는 별로 영향을 미치지 않는다. 단순히 확률이 과대평가될 가능성이 있다.

- 따라서 독립적이지 않은 evidence들이 많기 때문에 확률 추정치 자체가 정확하다고 볼 수는 없다.

    - 그렇기 때문에 실무자들은 확률의 실제값과는 관련이 없는, 단지 순위를 매기기 위해 Naive Bayes를 사용한다.

- 자연스럽게 점증적으로 학습한다. (incremental learner)

    - 한 번에 한 가지 훈련 사례를 모델에 업데이트 할 수 있다.

    - 새로운 훈련 데이터가 들어올 때 과거의 모든 훈련 데이터들을 재처리 할 필요가 없다.

    - 특히 새로운 라벨링 데이터가 들어올 때마다 모델을 업데이트하고자 하는 애플리케이션에 유리하다.

    - ex) creating a personalized spam email classifier

    - 사용자가 웹브라우저에서 '스팸'버튼을 클릭할 때 새로운 라벨링된 데이터가 들어온다. 그를 통해서 스팸 탐지 모델을 업데이트할 수 있다.

12. (ex) Weather Forecast

- 위와 같이 날씨에 따른 골프 가능 여부 데이터셋이 있다.

- 그럼 아래 사례의 클래스는 어떻게 예측할 수 있을까?

- 우선 모든 필요한 확률들을 계산해야 한다.

p(C | E) ≈ p(e1 | c) · p(e2 | c) · ... · p(ek | c)

- p(c)

- p(eᵢ | c) for "outlook"

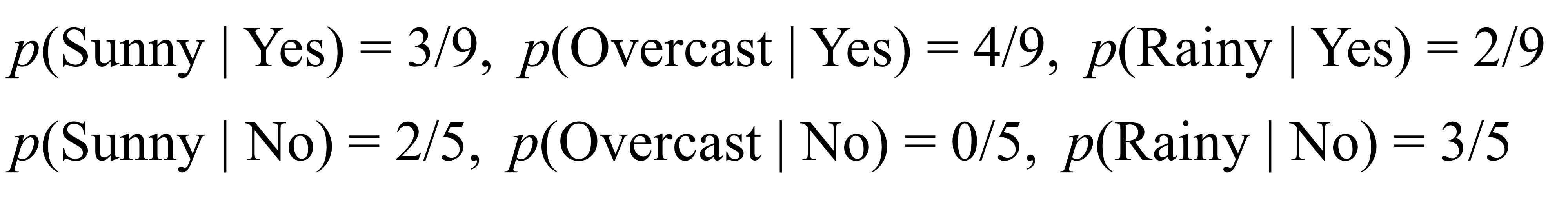
- p(eᵢ | c) for "temp"

- p(eᵢ | c) for "humidity"

- p(eᵢ | c) for "windy"

- compute p(c | E) for each class c

    - p(Yes | rainy, cool, high, true) ≈ p(rainy | yes) · p(cool | yes) · p(high | yes) · p(true | yes) · p(yes) = 0.00529

    - p(No | rainy, cool, high, true) ≈ p(rainy | no) · p(cool | no) · p(high | no) · p(true | no) · p(no) = 0.02057

- 정확한 확률값의 크기에 상관없이 Yes보다 No인 확률이 더 크기 때문에 play golf = No 로 결정된다.

13. (ex) Patient Diagnosis

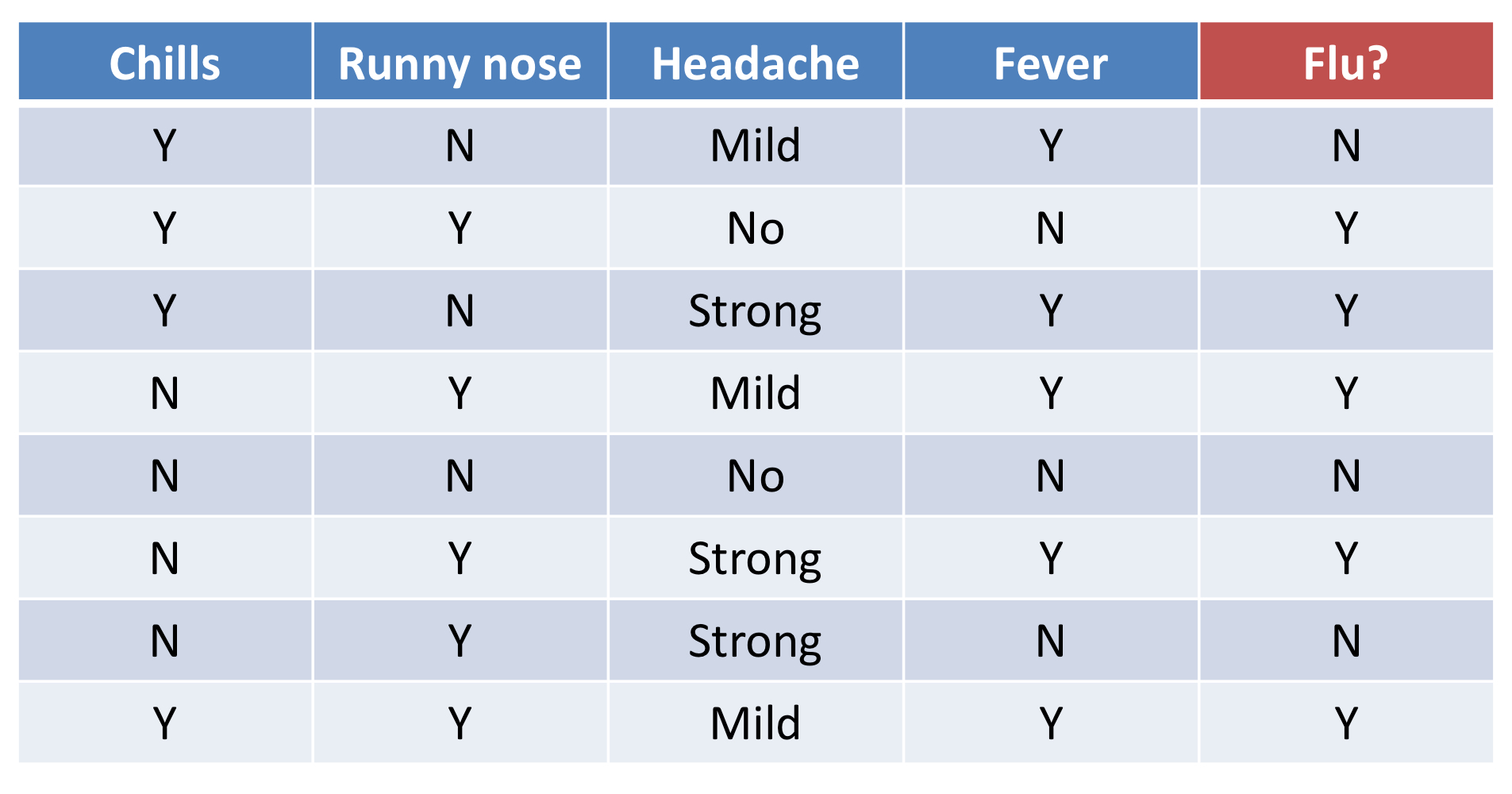
- 위의 예제와 같이 데이터셋을 통해서 flu 클래스를 예측해보고자 한다.

- p(c)

- p(eᵢ | c) for "chills"

- p(eᵢ | c) for "runny nose"

- p(eᵢ | c) for "headache"

- p(eᵢ | c) for "fever"

- compute p(c | E) for each class

    - p(flu = Y | chills = Y, runny nose = N, headache = Mild, feaver = N) = 0.006

    - p(flu = N | chills = Y, runny nose = N, headache = Mild, feaver = N) = 0.0185

- flu = N인 확률이 더 크기 때문에 Flu = N으로 결정된다.

14. (ex) Spam Detection

- p(c)

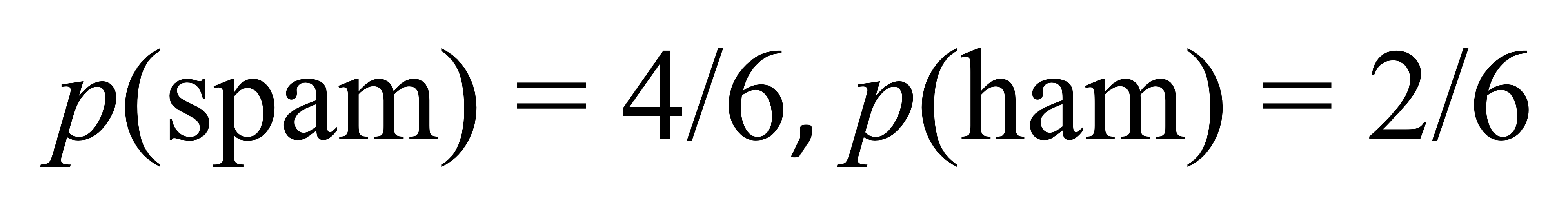
- p(eᵢ | c) for the word "password"

- p(eᵢ | c) for the word "review"

- p(eᵢ | c) for the word "send"

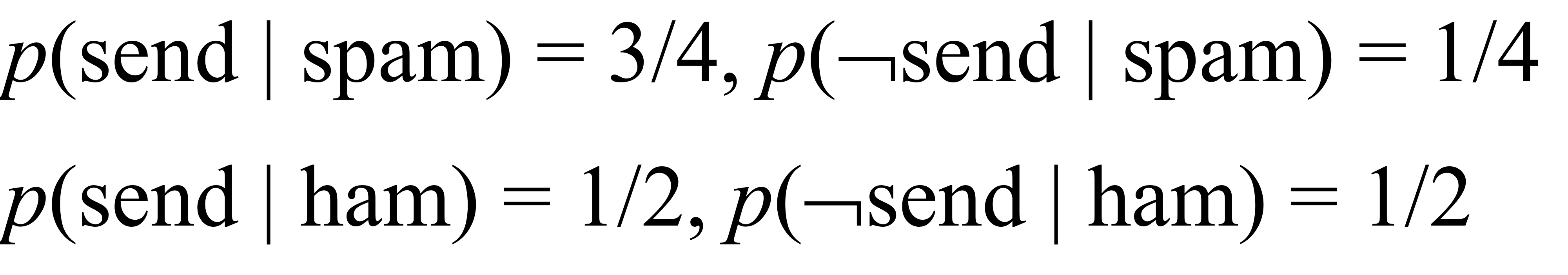
- p(eᵢ | c) for the word "us"

- p(eᵢ | c) for the word "your"

- p(eᵢ | c) for the word "account"

- compute p(c | E) for each class c

    - p(spam | ¬password, review, ¬send, ¬us, your, account) = 0.000976

    - p(ham | ¬password, review, ¬send, ¬us, your, account) = 0

- spam 일 확률이 더 크기 때문에 spam으로 결정된다.

15. A Model of Evidence "Lift"

- 전체 모집단에 대해 선택된 하위 모집단에서 positive class가 얼마나 더 만연한지 측정하는 classifier 평가지표이다.

- 즉, Lift = positive / sampling (targeting)

- evidence lifts의 하나로 Naive Bayes를 생각해볼 수 있다. 

- 변환한 식에서 p(eᵢ | c) / p(eᵢ) 가 클래스 c의 evidence lift이다.

- evidence lift는 eᵢ가 클래스 c를 얼마나 더 lift 시키는지, 클래스 c와 얼마나 연관성이 있는지, eᵢ가 이 개체를 클래스 c로 분류하는데 얼마나 도움이 되는지를 나타내는 지표이다.

- 사전확률 p(c)에서부터 시작하여 예시 E를 살펴볼 것이다.

- 각각의 증거 eᵢ는 클래스에 대한 확률을 높이거나 낮춘다. 

- 만약 liftc(eᵢ) > 1 이라면 확률은 증가할 것이고, liftc(eᵢ) < 1이라면 확률은 감소할 것이다.

16. (ex) Evidence Lifts from facebook 'likes'

- 최근 연구자들은 페이스북의 '좋아요'가 보통 직접적으로 드러나지 않는 사람들의 특징들을 꽤 예측한다는 논문을 발표했다.

- 지식 수준이 어떤지, 정신적인 상태는 어떤지, 이미 밝힌 동성애자인지, 술을 마시거나 담배를 피는지, 종교나 정치적 견해는 어떤지 등 말이다.

- 어떤 사람이 좋아요를 누른 기록과 각각 "High IQ"에 대한 evidence lifts이다. 

- "Sheldon Cooper"에 좋아요를 눌렀다는건 일반적인 사람들보다 '높은 IQ'를 갖고 있을 확률이 30% 더 높다는 의미이다.

- 마찬가지로 "Lord of the rings"에 좋아요를 눌렀다는건 일반적인 사람들보다 '높은 IQ'를 가지고 있을 확률이 69% 높다는 의미이다.

- 일반적으로 페이스북 인구에서 타겟 변수를 'IQ > 130'으로 잡으면, 약 14%의 사람들이 Yes 클래스에 해당한다는 가설이 있다.

- 그러면 아무것도 좋아요를 누르지 않은 경우엔 'IQ > 130'일 확률 추정치는 기본 비율인 14%이다.

- 만약 "Sheldon Cooper"에 좋아요를 눌렀다면, 확률 추정치는 0.14 x 1.3 = 18% 로 30% 증가된 값이 된다.

- 만약 (Sheldon Cooper, Star Trek, Lord of the Rings) 세 개에 좋아요를 눌렀다면, 확률 추정치는 0.14 x 1.3 x 1.39 x 1.69 = 43%가 된다. 

- 이처럼 evidence lift를 통해서 행동 특성을 예측할 수 있다.

수업 출처) 숙명여자대학교 소프트웨어학부 박동철 교수님 '데이터사이언스개론' 수업

1. Visualizing Model Performance

- 모델 성능을 시각화하기 위한 몇몇 유용한 기술들에 대해 다룬다.

- 모델 성능을 직관적으로 보여준다.

2. Ranking instead of Classifying

- 이전 장에서는 각 경우에 대한 결정을 expected value에 기반하여 어떻게 계산할 지 알아보았다.

- 이번에는 다른 전략으로 ranking에 대해 알아볼 것이다.

- 각 경우를 분리하여 결정하기보다는, 예측된 점수를 기반으로 사례들의 순위를 매긴 다음 상위 n개의 경우를 택하는 것이다.

- 많은 경우, 그저 가장 성능이 좋은 n개의 케이스를 원할 때가 있다. 예를 들어 캠페인을 위한 마케팅 예산이 이미 정해져 있는 경우가 그렇다.

- 이러한 경우 각 경우의 정확한 확률 추정치는 그닥 중요하지 않다.

- 정확한 확률값을 구하기보다 상대적인 순위를 통해서 가장 효율적인 몇가지 방법만 택하는 것이다.

3. Ranking Instances

- 개체에 점수를 매기는 classifier가 있다고 하자. 이때 점수는 확률값 (or distance)이다.

- ex) class probability(decision tree, k-NN classifier), distance from the separating boundary(support vector machine, logistic regression)

- 각 개체들을 점수에 따라 정렬한 후 특정한 값 T를 임계값으로 설정한다.

- 임계값을 높게 잡으면 정말 몇 개의 경우만 선택될 것이고, 임계값을 낮게 잡으면 가능한 많은 경우를 선택할 수 있을 것이다.

4. Thresholding Instances

- 임계값이 변할 때마다 true positive와 false positive의 수가 달라진다. 

- 따라서, 각 임계값마다 특정한 confusion matrix가 형성된다.

- 임계값을 기준으로 높은 순위는 'YES', 낮은 순위는 'NO'라고 예측하기 때문이다.

- 임계값이 낮아질수록 개체들은 N에서 Y로 옮겨진다. (예측값이)

    - (N, p) -> (Y, p), (N, n) -> (Y, n)

- 기술적으로, 각각의 임계값은 서로 다른 classifier를 생성한다.

- 그리고 각각의 confusion matrix를 통해 나타낸다.

- 그러면 다른 classifier에 의해 만들어진 순위는 서로 다른데 어떻게 비교해야 할까? 어떤 순위가 더 낫다고 볼 수 있을까?

- 또한, 적절한 임계값을 어떻게 찾을까? 

    - 이건 expected profit이 최대가 되는 임계값으로 결정할 수 있다.

5. Profit Curve

- 임계값에 따른 expected profit을 보여주는 곡선이다.

- 임계값이 낮아질수록 negative가 아니라 positive로 예측되는 개체들이 추가된다.

- 즉, 임계값이 낮아질수록 positive predict가 높아진다.

- 타겟 마케팅을 위한 3개의 classifier를 나타낸 profit curve이다.

- 각 곡선에 대해 고객들은 몇몇 모델에 기반하여 마케팅에 대해 응답할 확률에 따라 높은 확률부터 낮은 확률까지 정렬된다.

- 보통 고객의 비율에 대해 이야기할 것이다.

- x축은 임계값이고, y축은 그에 다른 이익이다.

- 곡선은 profit이 음수로 갈 수 있음을 보여준다. 항상 그런 것은 아니고 cost-benefit matrix에 따라 달라진다.

- 이윤이 작거나 응답자의 수가 작을 때 발생한다.

- 응답하지 않을 사람들에게 너무 많이 제공함으로써 비용을 너무 많이 지불하게 된다.

- 모든 곡선들은 같은 지점에서 시작해서 같은 지점에서 끝난다.

    - 0%는 지출도 없고 이익도 없는 상태이다.

    - 100%는 모든 사람들이 타겟이 된 상태이다. 따라서 모든 classifier가 같은 성능을 갖는다.

- 하지만, 그 사이에서는 classifier가 고객을 정렬한 방법에 따라 서로 다른 값을 갖는다.

    - 직선인 경우는 random model을 적용한 경우로 최악의 성능을 갖는다.

    - 위의 그래프에 따라 만약 마케팅에 예산이 정해져있어 8%의 고객에게만 제공할 수 있을 땐 x = 8 이내에서 가장 높은 값을 갖는 classifier 1을 선택하면 되고, 예산 상관없이 최고의 이익을 내고 싶다면 약 x = 50에서 가장 높은 값을 갖는 classifier 2를 선택하면 된다.

6. Two Limitation of Profit Curves

- 이전 장에서 본 조건부 확률을 이용하는 expected profit이다. 

- 이 값을 이용하기 위해서는 사전확률인 p(p)와 p(n)을 알고 있어야 하고, 그 값은 안정적으로 고정되어 있어야 한다.

- 또한, cost와 benefit (b(h, a), c(h, a))도 알고 있어야 하고 안정적으로 고정되어 있어야 한다.

- 하지만, 많은 실제 경우에서는 이 값들은 정확하지 않고 불안정하다.

    - ex) 사기 탐색의 경우 사기 금액이 정해져있지 않고 항상 변한다.

    - churn 관리의 경우 고객에게 제공하는 상품의 금액이 항상 다를 것이다.

7. Receiver Operating Characteristic (ROC) Graph

- 전체 공간에 성능 가능성을 보여줌으로써 불확실성을 수용할 수 있는 방법이다.

- calssifier에 의해 만들어지는 benefits (true positives) 과 costs (false positives) 사이의 상대적인 성능값을 보여준다.

- 각 점 (fpr, tpr) 은 classifier 한 개를 나타낸다.

- fpr = false positive rate (= FP / (FP + TN)) = 1 - specificity : negative 중에 틀린 것

- tpr = true positive rate (= TP / (TP + FN)) = sensitivity : positive 중에 맞은 것

- 점 A는 classifier A의 cost = 0.1, benefit = 0.4일 때의 성능을 나타낸다.

- (0, 0) : classifier가 무조건 N으로 예측한 것이다. false positive errors = true positives = 0

- (1, 1) : classifier가 무조건 Y로 예측한 것이다. 

- (0, 1) : 완벽한 classifier이다. 모든 negative와 positive를 올바르게 분류한다.

- (x, x) : positive class를 x · 100%로 랜덤으로 예측하는 classifier이다. 

    - (0.5, 0.5) : 랜덤으로 절반을 positive로 예측한다. positive를 절반 맞출 것으로 기대한다.

    - (0.9, 0.9) : 랜덤으로 90%를 positive로 예측한다. negative는 90% 틀리고, positive는 90% 맞을 것으로 기대한다.

- ROC space에서 c₁ 과 c₂를 비교해보자

    - c₁ 이 c₂에 비해 북서쪽 (왼쪽 위) 에 있으면 c₁이 더 낫다. true positive rate과 true negative rate이 모두 더 높거나 나쁘지 않다.

    - c₁ 이 c₂에 비해 남서쪽 (왼쪽 아래) 에 있으면 c₁이 더 보수적이다. false positive rate은 낮지만, true positive rate도 더 낮다. 틀리는 경우를 낮추는 model이다.

    - c₁ 이 c₂에 비해 북동쪽 (오른쪽 위) 에 있으면 c₁이 더 급진적이다. true positive rate도 높고 false positive rate도 높다. Y로 예측하는 개체를 늘림으로써 positive를 맞추는 경우에 더욱 집중하는 model이다.

- ranking model

    - 임계값에 따라 점수가 임계값보다 높으면 Y, 아니면 N으로 예측한다.

    - 각 임계값에 따라 ROC space에 다른 점들을 생성한다. 각 임계값에 따라 다른 confusion matrix가 생성되기 때문이다.

- 임계값이 낮아질수록 positive로 예측하는 개체들이 늘어나는데, positive instance와 negative instace를 모두 지나치게 된다.

- 따라서 true positive rate와 false positive rate이 모두 증가하기 때문에 곡선이 우상향한다.

8. Advantage of ROC Curves

- ROC Curve는 classifier가 사용될 조건으로부터 classifier 성능을 분리한다.

- 즉, 사전확률(p(p), p(n)) 과 costs and benefits(v(h, a))가 필요하지 않다는 것이다.

- 이러한 조건들이 바뀌어도 classifier의 위치와 상대적인 성능이 변하지 않는다.

- 사전 클래스가 달라지더라도 각 점의 위치는 달라질 수 있지만, curve의 모양 (다른 classifier 대비 상대적인 성능) 은 바뀌지 않는다.

9. The Area Under the ROC Curve (AUC)

- classifier의 ROC curve 아래의 면적이 간단히 1²의 일부로 표현된다. -> 0과 1의 범위 내로 표현된다.

- ROC Curve는 더 많은 정보를 제공하지만, AUC는 성능을 요약하여 하나의 숫자로 표현해야 할 때 유용하다.

- 왼쪽 그래프에서 숫자가 AUC이며 classifier의 성능을 나타낸다. 0.95는 0.85보다 10% 더 좋은 성능을 갖는다는 것이다.

- 오른쪽 그래프들에서 첫번째 그래프가 가장 성능이 좋고, 네번째 그래프가 가장 성능이 안좋은 classifier이다.

10. Cumulative Response Curve

- ROC Curve는 분류 모델 성능을 시각화하기 위한 일반적인 tool이다.

- 하지만, 개발자가 아닌 이해관계자들이 보기엔 너무 직관적이지 않다.

- Cumulative response curves는 더욱 직관적인 시각화이다.

- 임계값에 따른 타겟 개체의 true positive 비율을 함수로 표현한다.

- 따라서 YES 클래스를 얼마나 잘 분류하는지 시각화하는 그래프라고 볼 수 있다.

- false positive보다 true positive가 더욱 가치있기 때문이다.

- x축이 타겟 instance 비율, y축이 true positive rate이다.

- 임계값이 낮아질수록 더욱 많은 개체들을 타겟으로 한다.

- Random model : x%를 타겟으로 할 때 x%의 positives를 얻는다.

- A better model : x%를 타겟으로 할 때 x%보다 큰 positives를 얻는다.

- 따라서 그래프에서 대각선보다 위에 있는 그래프들은 더 나은 성능을 제공한다.

11. The Lift of a Classifier

- Lift : classifier가 random model (50%) 보다 얼마나 더 성능이 좋은지 나타내는 지표이다.

- 즉, 리스트에서 positive instance를 negative instace 위로 올리는 정도를 의미한다.

- Lift = (the percentage of positivie instances targeted) / (the percentage of instances targeted)

= 전체 타겟 개체들 중 positive 개체의 비율

(ex) 

- 100 customers (50 positives, 50 negatives)

- 리스트를 스캔해 내려가다가 중간에서 (50% targeted) 멈추면 얼마나 많은 positives가 있을 것으로 예상하는가?

- case 1 : sorted randomly

    - 절반의 positives가 있을 것이다. -> lift = 0.5 / 0.5 = 1

- case 2 : ordered by an effective classifier

    - lift > 1

- case 3 : perfect classifier

    - lift = 1 / 0.5 = 2

12. Lift Curve

- 타겟 개체의 비율에 대한 lift 값을 그래프로 표현한다.

- 기본적으로 주어진 x 점에서의 cumulative response curve 값을 해당 점에서의 대각선 값으로 나눈 값이다.

- 따라서, cumulative response curve의 대각선은 lift curve에서 y = 1의 수평선이 된다.

- ex) 'our model gives a two times lift'

    - 임계값을 선택할 때, 모델 타겟팅은 랜덤일 때보다 2배 더 낫다. (잘 맞춘다)

    - cumulative response curve에서 true positive rate은 random classifier의 true positive rate의 두 배일 것이다.

- 즉, lift는 타겟팅의 효과를 측정한다.

수업 출처) 숙명여자대학교 소프트웨어학부 박동철 교수님, '데이터사이언스개론' 수업

1. how measure a model?

- 데이터 분석을 통해 "얻고싶은 것"이 무엇인지 신중히 고려하는 것이 중요하다.

- 모델의 수행 능력을 의미있는 방식으로 측정해야 한다.

    - 각 문제에 대한 올바른 평가 방식은 무엇일까?

    - ex) 이동통신사 고객 이탈 문제 (celluar-churn problem) : 정확한 예측의 비율? 이탈한 고객의 비율?

2. Evaluation Classifiers (예측모델 평가)

- 알지 못하는 클래스에 대해 이미 갖고 있는 데이터를 바탕으로 예측하는 모델이다.

- 이진 예측 모델의 클래스: positive / negative

- 이러한 모델이 얼마나 잘 수행되는지 어떻게 평가할 것인가?

2-1. Plain Accuracy

- 지금까지 우리는 classifier의 성능을 측정하기 위한 간단한 지표를 가정했다. : accuracy (or error rate)

- accuracy = 예측 중 맞은 개수 / 전체 개수 = 1 - error rate

- 측정하기 쉽고 이해하기 쉽기 때문에 많이 쓰이는 방법이다.

- 하지만, 너무 간단하고, 몇 개의 문제점들이 있다.

2-2. Confusion Matrix

- n개의 클래스를 분류하기 위한 n x n 행렬이다.

    - 행(rows) : 예측값

    - 열(columns) : 실제 값

    - 다른 종류의 오차(error)들을 개별적으로 보여준다. : False positives, False negatives

- p, n이 실제 클래스에 속하는 값들이고, y, n이 예측한 값들이다. 

- 따라서 y-p에 속하는 값들은 y로 예측했는데 실제로 positive인 값들이다.

2-3. Problems with Unbalanced classes

1) 분류 문제에서 한 클래스가 rare하다고 생각해보자.

- 예를 들어, 사기당한 고객을 찾는 경우나, 결함이 있는 부품을 찾는 경우나, 광고 등에 응하는 고객을 찾는 경우 그런 경우들이 흔치 않기 때문에 클래스 분포가 불균형하거나 비스듬할 것이다.

- 이러한 경우에는 accuracy로 성능을 판단하기 어렵다.

- 예를 들어 클래스 값이 999:1 비율이라면, 항상 999의 개체가 속한 클래스를 선택한다면 정확도는 99.9%가 되기 때문이다. 

- 비율 불균형이 그리 크지 않더라도 정확도는 오해의 소지가 매우 크다. 잘못된 해석이 도출될 수 있다.

- ex) cellular-churn problem

- 1000명의 churn 예측 모델을 A와 B가 각각 만들었다고 하자. 

- A모델은 churn 클래스는 100% 예측하고, not churn 클래스는 60% 예측한다.

- B모델은 churn은 60%, not churn은 100% 예측한다.

- 이 경우 두 모델은 매우 다르게 작동하지만 accuracy는 80%로 똑같다.

2) 또한, accuracy는 테스트 셋에 따라 달라진다. 

3) false positive와 false negative를 구별하지 않는다.

- 둘을 같이 세기 때문에 오차들이 모두 똑같이 중요한 것처럼 여겨진다.

- 하지만, 이는 현실 세계에서는 드문 경우이다.

- 다른 종류의 오차는 다른 무게를 갖는다.

- ex) 의학 진단 경우

    - false positive : 실제로 병에 걸리지 않았지만 걸렸다고 진단한 경우 (기분은 나쁠 수 있지만 실제로 정상이기 때문에 괜찮음)

    - false negative : 실제로 병에 걸렸지만 걸리지 않았다고 진단한 경우 (대처를 못하기 때문에 훨씬 심각한 문제를 초래함)

- ex) cellular-churn 

    - false positive : 떠날거라고 생각해서 상품을 제공했지만 떠나지 않음 (어쨌든 고객을 유지했기 때문에 괜찮음)

    - false negative : 떠나지 않을거라고 생각해서 제공하지 않았지만 떠남 (고객을 잃었기 때문에 훨씬 손해임)

- 대부분의 경우, 우리는 false positive와 false negative를 다르게 다뤄야 한다.

- classifier에 의한 각 결정들의 cost나 benefit을 추정해야 한다.

- 일단 집계되면, 이러한 것들은 classifier에 대한 기대이익(or 기대비용) 추정치를 산출할 것이다.

2-3. Generalizing beyond classification

- 데이터사이언스를 활용할 때 목표가 무엇인지, 주어진 목표에 맞게 데이터마이닝 결과를 적절히 평가하고 있는지 중요하게 생각해야 한다.

- ex) Regression

    - 데이터사이언스팀이 영화 추천 모델을 만든다고 생각해보자. 

    - 평점은 1 - 5개의 별을 줄 수 있고, 모델은 사용자가 보지 않은 영화를 얼마나 많이 시작할지 예측한다.

    - 모델을 오차의 평균으로 측정해야 할까, 오차 제곱의 평균으로 측정해야 할까?

    - 더 나은 방법이 있는지 확인해야 한다.

3. Expected Value (EV) : Key Framework

- EV는 데이터 분석적 사고를 돕는 아주 유용한 개념적 도구이다.

- 데이터 분석 문제에 대한 생각을 정리하는데에 아주 유용한 핵심 프레임워크를 제공한다.

- 다음은 EV의 일반적인 계산식이다.

- o𝑖 : 가능한 결정 결과 (ex: classification -> YES or NO)

- p(o𝑖) : o𝑖의 확률

- v(o𝑖): o𝑖의 가치 (ex: cost, benefit or profit)

3-1. Using EV for Classifier Use (ex. 타겟 마케팅)

- 각 소비자의 클래스를 예측하여 더 응답할 가능성이 높은 고객들을 예측하고자 한다.

- 불행히도 타겟 마케팅의 경우 각 소비자가 응답할 확률은 대부분 1-2%로 매우 낮다.

- 그래서 우리가 상식적으로 응답할만한 소비자를 결정하기 위해 임계값을 50%로 정한다면 아마 아무도 겨냥하지 못할 것이다.

- 아마 모든 소비자가 '응답하지 않을 것'이라고 분류될 것이기 때문이다.

- 하지만, EV 프레임워크를 활용하면 문제의 핵심을 찾을 수 있을 것이다.

- feature vector가 x인 고객들에게 pᵣ(x)를 부여하는 모델을 갖고 있다고 가정하자.

    - pᵣ(x)는 고객 x가 응답할 확률의 추정치이다.

    - 예를 들면 classification tree, logistic regression model 등이 있다.

- 그러면 이제 다음과 같이 타겟 고객 x의 기대 수익 (or 기대 비용)을 계산할 수 있다.

    - vᵣ : 우리가 응답으로부터 얻는 가치 (value from a response -> profit)

    - vₙᵣ : 무응답으로부터 얻는 가치 (value from no response -> cost)

- example scenario

    - 상품가격 $200

    - 원가 $100

    - 마케팅비 $1

- EV 계산식에서 vᵣ = $99, vₙᵣ = -$1 

- 우리는 EV가 0보다 크기만 해도 이익을 얻는 것이다.

따라서 계산을 해보면 pᵣ(x) · $99 - (1 - pᵣ(x)) · $1 > 0

=> pᵣ(x) > 0.01 

- 고객 x가 응답할 확률이 1%만 돼도 남는 장사라는 것을 알 수 있다.

- 따라서 우리가 예상했던 50% 응답률이 아니라, 1% 보다 큰 확률 추정치를 갖는 고객을 타겟으로 삼아야 한다.

3-2. Using EV for Classifier Evaluation

- 지금까지 개개인의 결정에 주목했다면, 지금부터는 '결정의 집합'에 더욱 주목하고자 한다.

- 특히 우리는 모델로부터 만들어진 일련의 결정들을 평가해야 한다.

- 이 평가를 할 때 서로 다른 모델들을 비교하는 것이 필요하다.

    - 우리의 데이터 중심 모델은 직접 만든 모델보다 더 성능이 좋은가?

    - 분류 트리 모델이 로지스틱 회귀 모델보다 더 성능이 좋은가?

- 총체적으로 우리가 관심을 가지는 것은 각 모델이 얼마나 잘 수행하는지, 즉 그것의 expected value가 무엇인지이다.

- EV의 일반 계산식이다.

- 각 o𝑖는 예측 클래스와 실제 클래스의 가능한 조합 중 하나에 해당한다.

((Y,p),(Y, n), (N, p). (N, n))

- 그리고 p(o𝑖)는 이미 confusion matrix에 나와있다.

- 각 o𝑖는 confusion matrix의 각 셀에 해당한다.

- ex) 

1) step 1 : 각 케이스의 비율을 측정한다. (p(o𝑖))

- 각각의 count를 총 개체 수로 나눈다.

- p(h, a) = count(h, a) / T

    - h : 예측된 클래스 (Y / N)

    - a : 실제 클래스 (p / n)

    - T : 총 개체 수

    - count(h, a) : (h, a)케이스에 해당하는 개체 수

    - p(h, a) : (h, a)케이스의 비율 (or 확률 추정치)

2) step 2 : 각 케이스의 value를 명시한다. (v(o𝑖))

- 하지만, b(h, a)와 c(h, a)는 데이터로부터 추정할 수 없다.

- 이 둘은 일반적으로 분석으로부터 제공되는 외부 정보에 의해 정해진다.

- 그것들을 지정하는 것은 많은 시간과 노력이 필요하다. (ex: 우리가 고객을 유지하는 것이 정말 어느정도의 가치가 있는가?)

- ex) 위의 example scenario 예제

    - v(Y, n) = -1

    - v(N, p) = 0

    - p(Y, p) = 99

    - p(N, n) = 0

3) step 3 : total expected value (or profit) 을 계산한다.

- 다음 공식을 통해서 모델의 expected profit을 계산한다.

- final value는 각 고객 당 total expected profit을 나타낸다.

- 따라서 우리가 필요한 것은

    - 테스트 데이터셋에 대한 confusion matrix 계산

        - p(Y, p), p(Y, n), p(N, p), p(N, n)

    - cost-benefit matrix 생성

        - v(Y, p), v(Y, n), v(N, p), v(N, n)

3-3. Alternative Calculation of EV 

- alternative calculation은 종종 실제로! 사용되는 것이다.

- 왜냐하면 우리가 모델 비교 문제를 어떻게 다뤄야 하는지 정확히 알 수 있기 때문이다.

- 조건부확률

    - 사전 class : p(p) and p(n)

        - 각각 positive와 negative 개체일 확률이다.

    - p(x, y) = p(y) · p(x | y)

    - p(x | y) = p(x, y) / p(y)

        - (p(x, y) : x 와 y의 교집합)

- 다음과 같이 사전 클래스 p(p)와 p(n)을 찾아낼 수 있다.

- ex)

- expected profit = p(p) · [p(Y | p) · b(Y , p) + p(N | p) · b(Y , p)] + p(n) · [p(Y | n) · b(Y, n) + p(N | n) · b(N, n)]

    = 0.55 (0.92 · 99 + 0.08 · 0) + 0.45 (0.14 · -1 + 0.86 · 0) 

    ≈ $50.04

- 이를 통해 각 고객 당 평균적으로 약 $50 의 이익을 얻을 수 있다고 예측할 수 있다.

- 이제 경쟁 모델에 대한 정확도를 계산하는 대신에, expected values를 계산할 것이다.

- 나아가, 다양한 분포에 대해 두 모델을 쉽게 비교할 수 있다.

    - 각 분포에 대해 우리는 쉽게 사전확률을 대체할 수 있다.

    - 예를 들어, 불균형한 분포는 p(p) = 0.7, p(n) = 0.3 // 균등한 분포는 p(p) = 0.5, p(n) = 0.5라고 할 수 있다.

    - expected profit = p(p) · [p(Y | p) · b(Y , p) + p(N | p) · b(Y , p)] + p(n) · [p(Y | n) · b(Y, n) + p(N | n) · b(N, n)] 에서

       p와 n의 분포가 아무리 바뀌어도 [ ] 속에 있는 비율들은 변하지 않기 때문에 p(p)와 p(n)의 값만 바꾸어서 계산하면 된다.

    - p(p), p(n)을 제외한 다른 비율들이 변하지 않는 이유는 같은 모델이기 때문이다. 

4. Overview of the EV Calculation

5. Other Evaluation Metrics

- 데이터 사이언스에 사용되는 많은 평가 지표들이 있다.

- 모든 지표들은 근본적으로 confusion matrix의 요약본이다.

- Accuracy = (TP + TN) / (TP + FN + FP + TN) : 전체 개체 중 맞은 예측의 비율

- True positive rate (=Sensitivity) = TP / (TP + FN) = 1 - False negative rate : positive 중 맞춘 예측의 비율

- False negative rate = FN / (TP + FN) : positive 중 틀린 예측의 비율

- True negative rate (=Specificity) = TN / (FP + TN) = 1 - False positive rate : negative 중 맞춘 예측의 비율

- False positive rate = FP / (FP + TN) : negative 중 틀린 예측의 비율

- Precision 정밀도 = TP / (TP + FP) : positive 로 예측한 경우에서의 정확도

- Recall 재현율 = TP / (TP + FN) =True positivve rate (Sensitivity)

- F-measure F-값 = 2 x {(Precision x Recall) / (Precision + Recall)} : precision과 recall의 조화평균

- 이 세 가지는 정보 검색과 패턴 인식 (텍스트 분류) 에 널리 사용된다.

6. Baseline Performance

- 몇몇 경우, 우리는 모델이 어떤 기준선보다 더 나은 성능을 갖고있다고 증명해야 한다.

- 그렇다면 비교의 대상이 되는 적절한 기준선은 무엇일까?

    - 그것은 실제 용도에 따라 다르다.

    - 하지만 몇몇 일반적인 원칙들이 있다.

1) Random model

- 통제하기 쉬울 수 있지만, 그다지 흥미롭거나 유익하진 않을 것이다.

- 매우 어려운 문제나 처음 문제를 탐색할 때 유용할 것이다.

2) Simple (but not simplistic) model

- ex) weather forecasting

    - 내일의 날씨는 오늘과 같을 것이다.

    - 내일의 날씨는 과거부터 내일까지의 날씨의 평균일 것이다.

    - 각 모델은 랜덤으로 예측하는 것보다 훨씬 나은 성능을 발휘한다. 어떤 새롭고 더욱 복잡한 모델도 이것들보다는 나은 성능을 가져야 한다.

3) The majority classifier 다수결

- 항상 훈련 데이터셋에서 다수의 클래스를 선택하는 방법이다.

- 우리는 모집단의 평균 값이라는 직접적으로 유사한 기준선을 가지고 있다. 

- 보통 평균이나 중간값을 사용한다.

- ex) 추천 시스템    - 특정 영화가 주어졌을 때 고객이 몇개의 별점을 줄 지 예측해보자.    - random model     - simple models        - model 1 : 고객이 영화들에게 준 별점의 평균 값을 사용할 것이다.        - model 2 : 대중이 그 영화에 준 별점의 평균 값을 사용할 것이다.    - combination of multiple simple models : 이 둘에 기초한 간단한 예측은 둘 중 하나를 따로 사용하는 것보다 훨씬 낫다.

- 간단한 모델을 비교하는 것 외에도, 배경 지식을 기반으로 한 간단하고 저렴한 모델을 기본 모델로 사용할 수 있다.

- ex) Fraud detection 사기 탐지    - 일반적으로 대부분 사기당한 계정들은 갑자기 사용률이 늘어난다고 알려져 있다.    - 거래량 급상승에 대한 계좌 조회는 많은 사기를 잡기에 충분했다.    - 이 아이디어를 구현하는 것은 간단하며, 유용한 기준선을 제공했다.

수업 출처) 숙명여자대학교 소프트웨어학부 박동철 교수님 '데이터사이언스개론' 수업

[Similarity]

1. Similarity (유사도)  -> "거리" 개념

: 많은 데이터 사이언스 방법과 솔루션들의 근본이 된다.

- ex) 비슷한 것들 검색, 비슷한 것들 그룹화 (클러스터링), 상품 추천, 비슷한 케이스로부터의 추론

- objects 간의 "거리"를 이용해서 유사도 측정

- 각각의 object를 feature vector로 표현 -> 두 벡터간의 유클리드 거리 계산

* Euclidean Distance 유클리드 거리

- 두 점 사이의 직선 거리를 계산하는 보편적인 방법

- d(A, B) = √ {(a₁-b₁)² + (a₂-b₂)² + ... + (aₙ-bₙ)²}

[Neighbors]

2. Nearest-Neighbor Reasoning (NN)

- Nearest-Neighbor : 가장 유사한 개체들

- 우수한 기업고객과 가장 유사한 기업 탐색, 온라인에서 기업의 소매 고객과 가장 유사한 고객 탐색 등  

    -> 영업인력 직접적으로 도움, 타겟 마케팅

- ex) 위스키 분석 

    - 며칠 전 저녁에 맛 본 "Bunnahabhain" 위스키가 마음에 들었다고 하자. 다른 single malt 위스키들 중 유사한 것을 어떻게 찾을 수 있을까?

    - 각각의 single malt 위스키들을 feature vector로 나타낸다. 그리고 저 위스키와 가장 가까운 이웃을 찾는다.

    - 이처럼 각각의 특징들을 숫자 형태로 나타낸다.

    - 그러면 이처럼 특징들을 바탕으로 다른 위스키들과의 거리를 구할 수 있다. "Glenglassaugh"가 가장 유사하다고 볼 수 있다.

- Nearest Neighbors for Predictive Modeling

    - 타겟 변수를 예측하고자 하는 새로운 데이터가 주어진다.

    - 훈련 데이터셋으로부터 가장 유사한 데이터들을 선택한다.

    - 그들의 타겟 값들에 기반하여 새로운 데이터의 타겟 값을 예측한다.

3. Classification Using NN

- 새로운 데이터의 클래스(label)을 어떻게 예측할 수 있을까? (이웃을 이용하여 새로운 개체 분류)

- k개의 가장 가까운 이웃들을 찾는다.

- 그들의 타겟 변수를 참조한다.

    예를 들어, k=3이고, 두 개의 타겟 값은 (+), 한 개의 타겟 값은 (-)이면 다수결에 의해 (+)으로 예측할 수 있다.

- ex) 신용카드 마켓팅 문제

    - 아래 자료에 근거하여 David가 신용카드 제안에 응답할 지 예측한다.

    - 거리가 가까운 3명의 이웃을 찾을 수 있다. (Rachael, John, Norah)

    - 그들의 타겟 값을 이용하여 다수결로 예측하면 Yes로 예측할 수 있다.

4. Probability Estimation Using NN

- 새로운 데이터가 클래스에 속할 확률을 어떻게 구할 수 있을까?

- k개의 가장 가까운 이웃을 찾는다.

- 각 클래스의 빈도 비율을 계산한다.

    예를 들어, k=3일 때 Yes가 두 명, No가 한 명이면 Yes에 속할 확률은 2/3(66.7%), No에 속할 확률은 1/3(33.3%)로 계산할 수 있다.

5. Regression Using NN

- 새로운 데이터의 값을 어떻게 측정할 수 있을까? 

- k개의 가장 가까운 이웃들을 찾는다.

- 그들의 타겟 값들의 평균(or 중간값)을 계산한다.

    예를 들어, 위의 자료에서 David의 수입을 예측하고자 한다. Rachael, John, Norah의 수입이 각각 50, 35, 40이기 때문에 평균은 42, 중간값은 40으로 예측해 볼 수 있다.

6. NN의 두가지 이슈

1) 몇 개의 이웃을 선택해야 하는가?

    - nearest neighbor 알고리즘은 종종 k-nn 으로 불린다.

    - k를 결정하는 데에 관한 간단한 답은 없다. *_* 

    - 다수결을 활용하기 위해서 홀수로 정하는 것이 좋다.

    - k가 클수록 추정치가 더욱 평준화된다. outlier의 영향을 덜 받기 때문에 나쁘지 않다.

    - k = n이면 전체 데이터셋이 예측에 활용되기 때문에

        - classification 에서는 항상 가장 많은 값의 클래스에 속할 것이고,

        - regression 에서는 타겟 값이 항상 모든 값들의 평균으로 예측될 것이며,

        - class probability estimation 에서는 항상 base rate 확률로 예측될 것이다.

2) 모든 이웃들을 동일하게(평등하게) 간주해야 할까?

- 몇몇의 가까운 이웃들은 다른 가까운 이웃들보다 더욱 가까울 수 있다.

- 다수결 예측이나 평균을 구할 때 문제가 된다.

    - 이들은 이웃이 새로운 데이터와 얼마나 가까운지는 고려하지 않는다.

    - 위의 David 예제에서 k=3 일 때에는 세개의 데이터들의 거리가 모두 15 근처로 비슷하다. 하지만 k=4 로 정하면 4번째 가까운 이웃과의 거리는 122가 되기 때문에 다른 3개의 이웃들과는 많이 차이가 난다. 이를 동일하게 취급하는 것은 문제가 있다.

- 이를 해결하기 위해서는 유사도에 따른 가중치를 부여하면 된다. 

    - 다수결을 이용할 때 모든 표를 1로 정하지 않고, w₁ x 1 + w₂ x 1 + w₃ x 1 + ... 의 형태로 구한다.

    - wᵢ 는 유사도에 비례하여 할당되며, 보통 Σwᵢ = 1이 되도록 설정한다.

    - 평균을 구할 때에도 값을 더할 때 가중치를 곱하여 더한다.

    - (w₁ v₁ + w₂ v₂ + ... wₙ vₙ) / n

    - 마찬가지로 wᵢ 는 유사도에 비례하여 할당되며, 보통 Σwᵢ = 1이 되도록 설정한다.

- ex) weighted voting, k = 4

    - 각 가중치를 1/distance² 으로 구한다. 제곱을 하는 이유는 이상치의 가중치를 낮추기 위해서이다.

    - 그리고 비율을 따져서 가중치들의 합이 1이 되도록 한다. 

    - 위와 같이 가중치를 이용하여 비율을 구할 수 있고, Yes의 값이 더욱 크기 때문에 Yes라고 예측할 수 있다.

7. Geometric Interpretation of NN (NN의 기하학적 해석)

- 명시적으로 경계가 형성되진 않지만, 각 점의 분류를 결정함으로써 암시적은 영역을 계산할 수 있다. 

- k=1 로 분류한 그래프이다. k=1인 경우 자기 자신만을 그룹으로 가지며 정확도는 100%이다. 따라서 overfitting이 된다.

- 그래프 관찰

    - 경계들은 불규칙적이며, 특정한 기하학적 모양을 찾아볼 수 없다.

    - 훈련 데이터셋의 개체를 둘러싼 경계는 매우 구체적이다.

    - 경계는 이상치에 매우 민감하다. 위의 그래프에서 '+' 사이에 있는 '·' 의 경우가 그렇다.

7. Overfitting & Complexity Control of NN 

- 1-NN 

    - 훈련 포인트 자체는 자기 자신으로 예측되며, 자기 자신이 가장 가까운 이웃으로 검색된다.

    - 그러므로 1-NN 은 overfitting이 매우 강하게 발생한다.

- k-NN 

    - k는 복잡도 파라미터이다. (complexity parameter)

    - 극도로 복잡하게 만드려면 k = 1로 지정할 수 있다. 

    - 다른 경우에는 k = n이 된다. 그러면 모든 모델에서 그다지 복잡하진 않을 것이다.

- k를 선택하는 방법은 모델에 따라 다르다.

- 일반적인 방법

    - 다양한 k값에 따른 중첩 교차 검증을 실시한다.

    - 테스트셋에서 가장 좋은 성능을 보여준 k를 선택한다.

    - 전체 훈련 데이터셋에 대한 k-NN 모델을 형성한다.

    - 선형 모델이나 트리 구조 모델에서 경계는 부드러운 곡선이나 일정한 조각의 기하학적 영역이 아니다.

9. NN 모델의 이슈

1) Intelligibility 명확성 (얼마나 이해하기 쉬운가)

- 단일 인스턴스가 어떻게 결정되는지 설명하는 것은 쉽다.

- 하지만, 데이터로부터 어떤 '지식'이 도출되었는지 설명하는 것은 어렵다.

    - 데이터로부터 어떤 시스템을 배웠는지, 어떤 근거로 결정을 내렸는지

- 따라서, 모델에 정당성을 부여하는 것이 중요할 땐 k-NN은 바람직하지 않다.

2) Computational efficiency 계산 효율

- 훈련시키는 것은 매우 빠르게 진행된다.

    - 보통 저장된 개체들만 활용하기 때문에 모델을 만드는데 큰 노력을 들일 필요가 없다.

- 하지만, 예측/분류는 많은 노력과 시간이 필요하다.

    - 데이터베이스에서 새로운 개체와 가장 가까운 이웃들을 찾아야 하기 때문이다.

- 따라서, k-NN 방법은 실시간 적용에 활용하기엔 실용적이지 않을 수 있다.

10. 이질적인 속성들을 다루는 기술

1) 범주형 속성을 어떻게 다룰 것인가?

- 범주형 속성을 숫자형으로 바꾼다. 

- ex) Sex: Male / Female -> 0 / 1

- 이진 변수는 바꾸기 쉽지만, 여러개의 값은 어떻게 바꿔야할까?

2) 값이 큰 변수들은 거리에 매우 큰 영향을 미친다.

- 따라서 변수들의 범위와 규모(축척)을 측정해야 한다.

- ex) Age : [0, 100] , Income : [0, 100,000] -> Age : [0, 1], Income : [0, 1]

11. 거리를 구하는 다른 함수들

11-1. Euclidean distance (L2 norm)

- 가장 많이 사용되는 거리 함수

- 직관적이고 계산하기 쉽다.

11-2. Manhattan distance (L1 norm)

- 격자에서 이동한 거리의 총합

- ex) d((3,4), (5,2)) = |3-5| + |4-2| = 4

11-3. Jaccard distance 

- 두 집합의 유사도를 측정하는 방법이다.

- 두 집합이 공통적인 요소를 많이 가질수록 거리가 감소한다.

11-4. Cosine distance

- 두 벡터 사이 각의 cos값을 측정하는 방법이다.

- 특히 벡터의 크기를 무시하고자 하는 경우 유용하다.

- 텍스트 분류를 통해 두 문서 사이의 유사도를 측정하고자 할 때 종종 사용된다.

[Clustering]

12. Clustering (군집화)

- 비슷한 개체들끼리 자연스럽게 맺어지는 그룹을 찾는 방법이다.

- 특정한 타겟 속성이 없다.

- unsupervised segmentation (비지도 분할) 이라고도 부른다.

- ex) 더 나은 서비스를 위해 고객 그룹화, 더 보기 좋게 진열/정리 하기 위해 상품 그룹화

- 그룹 내의 개체들은 비슷하며, 서로 다른 그룹의 개체들은 그다지 비슷하지 않다.

- 지도 모델은 알고있는 데이터의 타겟 변수 값을 기반으로 특정한 타겟 변수 값을 예측하기 위한 패턴을 발견하는 것이다.

- 비지도 모델은 데이터셋에서 타겟 변수에 초점을 맞추지 않고, 다른 종류의 정규성을 찾는 모델이다.

- ex) 위스키 분석 (위의 예제)

    - 이번엔 '맛'이 비슷한 위스키끼리 클러스터링을 해보려 한다.

    - 계층적 클러스터링, k-means 클러스터링을 고려해볼 수 있다.

 13. Hierarchical Clustering 계층적 클러스터링

- 각 개체의 고유한 클러스터에서 시작한다.

- 반복적으로 가장 가까운 클러스터끼리 합친다. 

    - 유사도나 거리함수를 이용한다.

- 이론적으로는 하나의 클러스터가 될 때까지 반복한다. 하지만 통상적으로 이정도로 많이 반복하지는 않는다.

14. 클러스터 사이의 거리 (distance function = linkage function)

1) Min distance

- 각 클러스터에서 가장 가까운 점 사이의 유클리드 거리

2) Centroid distance  

- 클러스터의 중간(모든 데이터들의 '평균값') 사이의 유클리드 거리 

15. Dendrogram 계통도

- 클러스터의 계층을 명시적으로 보여주는 그림

- 계통도를 수평으로 잘라서 원하는 수의 클러스터를 구할 수 있다. 

- 이를 통해 언제 클러스터링을 멈출 지 알 수 있다.

- 아래로 갈수록 클러스터의 수가 늘어난다.

16. 계측적 클러스터링의 장점

- 클러스터의 수를 결정하기 전에 이미 계통도를 통해 그룹화가 된 것을 볼 수 있다.

- 원하는 수의 클러스터에서 계통도를 자를 수 있다. (클러스터링을 멈출 수 있다.)

17. ex) Hierarchical Clustering of Scotch Whiskeys

- 클러스터는 스코틀랜드의 지역과 완전히 일치하지는 않다.

- 단순히 잘 알려진 것을 구입하는 대신, 각자의 클러스터에서 선택할 수 있다.

- 혹은 다른 '가장 비슷한' 위스키를 추천하는 가이드를 만들 수도 있다.

18. k-Means Clustering 

- k개의 그룹을 만드는 클러스터링 알고리즘이다.

- 가장 유명한 centroid-based clustering algorithm 이다.

- k는 데이터에서 찾은 클러스터의 개수이다. (사용자에 의해 특정된다.)

- means는 중심을 뜻한다. 클러스터에 속한 점들의 '평균값'을 의미한다.

19. k-Means Algorithm

- 초기 k개의 클러스터 중심을 고른다. (보통 랜덤으로 정한다.)

- 각 점을 그로부터 가장 가까운 중심이 해당하는 클러스터에 할당한다.

- 모든 점들이 할당된 이후, k개의 클러스터의 중심을 갱신한다.

- 그리고 다시 모든 점들을 그들의 가장 가까운 클러스터에 재할당한다.

- 더 이상 점들이 클러스터를 이동하지 않고 안정될 때까지 3-4번 반복한다.

- 각 중심들이 클러스터의 결과이다.

- 각 점들은 각각의 클러스터에 소속되어 있다.

20. ex

- 90개의 점을 k=3으로 하여 클러스터링 하는 과정이다.

- 분홍색, 초록색, 파란색 선은 각각 클러스터의 중심이 이동한 경로이다.

- 경로의 끝에 까만 점이 최종 클러스터의 중심이다.

21. Initial k Centroids 고르기

- k-means 알고리즘을 한 번 돌리는 것은 최상의 클러스터링이 아닐 것이다.

    - 초기 중심의 위치가 클러스터링의 결과를 만들게 되기 때문이다.

- 해결책은 초기의 랜덤 중심부를 다르게 하여 여러번 k-means 알고리즘을 돌리는 것이다.

- 그렇게 나온 결과들 중 가장 클러스터링이 잘 된 결과를 선택한다.

- 가장 좋은 클러스터링은 클러스터의 평균 직경을 최소화하는 것이다. (각 점에서부터 중심까지의 거리의 평균)

22. 올바른 k 값 고르기

- 실생활에서 최적의 k 값을 고르는 방법은 알 수 없다.

- 하나의 간단한 전략은, k-means 를 여러번 돌려서 가장 클러스터링이 잘 된 k를 고르는 방법이다.

- 그것은 클러스터의 평균 직경이 작고, 클러스터의 수가 그리 많지 않은 것이다.

- 다음 그래프에서는 기울기가 완만해지는 지점인 k = 3이 가장 좋은 k이다.

23. ex) Clustering business news stories

- 문서들을 단어들의 집합으로 나타낸다.

- Jaccard distance 를 이용하여 두개의 문서 사이의 거리를 구한다. (1-교집합/합집합)

24. ex) Clustering wiskey

- 각 위스키의 feature vector를 나타낸다 (1, 0, 1, 1, 0, ...)

- 두 위스키 사이의 거리를 유클리드 거리로 구한다.

수업 출처) 숙명여자대학교 통계학과 "통계수학" 수업, 윤재은 교수님

1. 행벡터와 열벡터

A(nxm)

- 행벡터 : A의 행에서 만들어지는 벡터 → n개 만들 수 있다.

  r₁' = (a₁₁, a₁₂, ..., a₁ₘ)

  r₂' = (a₂₁, a₂₂, ..., a₂ₘ)

...

  rₙ' = (aₙ₁, aₙ₂, ..., aₙₘ)

* A의 행에서 얻어지는 벡터 r₁, r₂, ..., rₙ를 선택하여 선형독립이 되도록 최대한 모았을 때 벡터의 개수

- 열벡터 : A의 열에서 만들어지는 벡터 → m개 만들 수 있다.

  c₁ = (c₁₁, c₂₁, ..., cₙ₁)'

  c₂ = (c₁₂, c₂₂, ..., cₙ₂)'

...

  cₘ = (c₁ₘ, c₂ₘ, ..., cₙₘ)'

* A의 열에서 얻어지는 벡터  c₁, ..., cₘ를 선택하여 선형도립이 되도록 최대한 모앗을 때 벡터의 개수

2. rank

- 모든 행렬에서 계산 가능

Th6.3 > 임의의 행렬 A(mxn)에서 다음 두 수는 동일하다.

    - 행으로 만든 벡터를 선택하여 선형독립이 되도록 최대한 모았을 때 벡터의 수

    - 열로 만든 벡터를 선택하여 선형독립이 되도록 최대한 모았을 대 벡터의 수

- 그 수를 행렬 A의 rank로 정의

3. rank 성질

- rank(A)는 양의 정수이며, 영행렬의 rank는 0으로 정의한다.

- rank(Amxn) ≤ min(m, n)

- rank(Anxn) = n : 최대계수를 갖는다. → A가 정칙행렬

- rank(Anxn) < n : 최대계수를 갖는지 않다. → A가 비정칙행렬

Th6.4 > rank(A) = rank(A')

= rank(A'A) = rank

Th6.5 > rank(AB) ≤ min { rank(A), rank(B) }

수업 출처) 숙명여자대학교 통계학과 "통계수학"수업, 윤재은 교수님

1. 직교벡터

두 n차원 벡터 x, y에 대해서 x · y = 0일 때, x와 y는 서로 수직이다.

단위벡터는 벡터를 벡터의 노음(길이)으로 나눔으로써 만들 수 있다.

norm = ||x|| = √(x ·x)

단위벡터 z = 1/||x|| x

* 직교집합 : n차원 벡터 집합 S = {x₁, x₂, ..., xₚ} 에 속해있는 임의의 두 벡터가 서로 직교일 때,

즉 모든 𝑖, 𝑗에 대해서 x𝑖' x𝑗 = 0 일 때, S를 직교집합이라고 한다.

* 정규직교집합 : 직교집합 S에 속하는 모든 벡터가 단위벡터일 대,

즉 ||x𝑖|| = 1일 때 S를 정규직교집합이라고 한다.

- (ex) S = {(1 0 0)T, (0 1 0)T, (0 0 1)T}

Th5.1 > 영벡터가 아닌 n차원 벡터 x₁, x₂, ..., xₚ 가 직교집합이면 이 벡터집합은 선형독립이다.

pf) a₁x₁ + a₂x₂ + ... + aₚxₚ = 0

양 변에 x₁ 을 곱하면

a₁x₁·x₁ + a₂x₂·x₁+ ... + aₚxₚ·x₁ = 0

직교집합이기 때문에 x₁·x𝑖 = 0

따라서 a₁, a₂, ...., aₚ = 0 -> 선형독립

* 직교행렬 : 정규직교 열들로 구성된 정방행렬

2. 정사영

p = ka

b - p ㅗ a

(b - p) · a = 0

(b - ka) · a = 0

b · a - ka · a = 0

k = b · a / a · a

∴ p = (b · a / a · a) · a

* 벡터 b의 평면 V 위로의 정사영 p

( A = (a₁ a₂)T )

TH5.3 > 선형독립인 a₁ , ..., aₚ 에 의해 생성되는 벡터공간을 V라고 할 때, 벡터 b의 V로의 정사영 p는 p = A (A'A)⁻¹ A' b 을 만족한다.

수업출처) 숙명여자대학교 통계학과 '통계수학' 수업, 윤재은 교수님

1. n차원 벡터, 벡터합, 내적

- 스칼라 : 크기만 있고 방향을 가지지 않는 양

- 벡터 : 크기와 방향 모두 가지고 있는 양

** ℝⁿ 의 두 벡터 x = (x1, x2, ..., xn)' 과 y = (y1, y2, ..., yn)' 의 내적은

x · y = Σ x𝑖 y𝑖 = x1y1 + ... + xnyn = xTy = yTx

** 벡터 x = (x1, x2, ..., xn)'의 길이 (노음, norm)은 ||x||로 표시하고, ||x|| = √(x · x) = √(Σx𝑖²) 이다.

** 두 벡터 x = (x1, x2, ..., xn)' 과 y = (y1, y2, ..., yn)' 사이의 거리

d(x, y) = ||x - y|| = √(x - y) (x - y) = √(Σ(x𝑖 - y𝑖)²)

** 내적의 기하학적 의미 x · y = ||x|| ||y|| cosθ

** x · y = 0 이면 두 벡터는 직교 (x ㅗ y)

** 두 벡터가 이루는 각을 θ라고 하면 cosθ = x · y / ||x|| ||y||

** 임의의 n차원 벡터에 대해 다음이 성립한다. <x, y> = x · y

> <x, y>² ≤ <x, x> <y, y>

> ||x + y|| ≤ ||x|| + ||y||

2. 선형독립과 선형종속

: x1, x2, ..., xm이 n차원 벡터들이며, a1, a2, ..., am 이 스칼라일 때

u = a1 x1 + ... + am xm 형태의 합을 x1, x2, ..., xm 의 선형결합 이라고 한다.

어떤 벡터가 다른 벡터들의 선형결합으로 얻어질 수 있는지 규명하는 것이 중요하다.

ex) 3차원 벡터

x1 = (3, 0, 1)', x2 = (2, -1, 3)', x3 = (5, 0, 4)' 의 선형결합으로 y = (1, 3, -2)' 표현하면

y = (-1) x1 + (-3) x2 + 2 x3

벡터들의 집합 S = {x1, x2, ..., xm}에서 a1 x1 + ... + am xm = 0 을 만족하는 a𝑖 들의 값이 a1 = a2 = ... = 0만 존재한다면 S는 선형독립이라고 한다.

만약 적어도 하나는 0이 아닌 a𝑖 가 존재한다면 S는 선형종속이라고 한다.

즉, S가 선형독립이면 어떠한 벡터도 다른 벡터들의 선형결합으로 표시될 수 없다. 

S가 선형종속이면 어느 한 벡터가 다른 벡터들의 선형결합으로 표시될 수 있다.

이를 규명할 때에는 a1 x1 + ... + am xm = 0 형태로 놓고 a𝑖에 대해 연립방정식을 풀면 된다.

a𝑖가 모두 0이 나오면 선형독립인 것이고, a𝑖끼리의 관계식이 나온다면 선형종속인 것이다.

Th4.1 > 두 개 이상의 벡터로 구성된 벡터 집합 S = {x1, x2, ..., xm} 이

> 선형종속이기 위한 필요충분조건은 S에 속하는 벡터 중 적어도 하나의 벡터가 다른 벡터의 선형결합으로 표현 가능한 것이다.

> 선형독립이기 위한 필요충분조건은 S에 속하는 어떤 벡터도 다른 벡터의 선형결합으로 표현될 수 없는 것이다.

Th4.2 > 두 벡터만을 갖는 집합이 선형종속이기 위한 필요충분조건은 적어도 이들 벡터 중 하나가 다른 벡터의 실수배로 되는 것이다.

* n차원 벡터를 선형독립이 유지되도록 모았을 때 최대한 모을 수 있는 개수는 n개이다.

* n차원 벡터를 n+1개 이상 모으면 무조건 선형종속이 된다.

3. 벡터공간 

V 를 벡터들을 모아놓은 집합이라고 할 때, V의 모든 원소 x, y에 대해 다음의 두 성질이 만족하면 V를 벡터공간이라고 한다.

(v1)  x ∈ V, y ∈ V → x + y ∈ V      : 덧셈에 대해 닫혀있다

(v2)  x ∈ V → ax ∈ V                     : 곱셈에 대해 닫혀있다

ex) V = {(x, y, z) : x + y + z = 0} 

(v1)  V1 = (x1, y1, z1)' ∈ V, V2 = (x2, y2, z2)' ∈ V

V1 + V2 = (x1 + x2, y1 + y2, z1 + z2)'

(x1 + x2) + (y1 + y2) + (z1 + z2) = (x1 + y1 + z1) + (x2 + y2 + z2) = 0 ∈ V

(v2) a(x1 + y1 + z1) = 0 ∈ V

벡터공간 V = R³의 임의의 원소 z = (z₁ z₂ z₃)T가 x₁ x₂ ·x₃

벡터공간을 생성하면서 선형독립인 벡터들의 모임을 "기저"라고 한다. 

벡터공간의 기저는 유일하지 않다.

수업 출처) 숙명여자대학교 소프트웨어학부 수업 "데이터사이언스개론", 박동철 교수님

1. Overfitting

- 데이터 사이언스에서 가장 중요한 근본 개념 중 하나이다.

- 모델을 만들 때 너무 flexible하게 만들면 모델이 특정한 데이터셋(훈련 데이터셋)에 너무 적합해진다.

- 모델이 훈련 데이터셋을 넘어선 일반적인 데이터셋에는 잘 적용되지 않는 경우이다.

- 모델은 새로운 데이터 개체도 잘 예측해야 한다.

2. 근본적인 부작용

- 더 복잡한 모델을 사용하면 정확도는 높아지겠지만, outfitting의 가능성 또한 높아진다.

- 한번에 overfitting을 제거할 방법은 없다.

- 가장 좋은 전략은 overfitting을 인지하고, 원칙적인 방법으로 복잡도를 조절하는 것이다.

- fitting graph : 복잡도 함수로써 모델의 정확도를 보여주는 그래프이다.

- 보통 모델을 만들 때 훈련 데이터에서 일정 부분을 holdout data로 빼놓고 훈련 데이터로 모델을 만든 다음 정답을 알고 있는 테스트 데이터로 정확도를 평가한다.

- 조금 더 general한 정확도를 측정할 수 있다.

- 위의 그림에서 오른쪽이 fitting graph이다.

3. overfitting 인지

- 모델이 충분히 복잡하지 않을 때 : 훈련데이터와 테스트 데이터 모두에서 정확도가 낮다. → underfitting

- 모델이 너무 복잡해질 때 : 훈련데이터에서는 정확도가 높아진다. 하지만, 테스트 데이터에서는 정확도가 낮아진다. → overfitting

- (ex) : customer churn table model.

    - 극단적인 예시는 fitting graph가 독특할 것이다.

    - 행의 개수가 많을수록 복잡도가 커질 수 있다.

    - learning에 'churn' data만 넣고, 여기에 없는 데이터는 'stay' data로 인식하도록 했다.

    - 모델이 증가하면서 훈련 데이터의 에러는 감소하지만, 테스트 데이터의 에러는 어느 특정 값에서 시작해서 변하지 않는다.

    - 이유 : 학습을 할 때 churn data만 put했다. 그러면 테스트 데이터는 그 안에 포함되어 있지 않기 때문에 모두 'stay' data로 인식한다. 하지만 그 중에 churn data가 있을 것이다. 따라서 (holdout 'churn' data) / (holdout data) 의 값이 holdout data의 base error rate (=b) 가 된다.

4. overfitting in tree induction

- 극단적인 classification tree : 모든 leaf node들이 pure할 때까지 데이터를 나눈 tree

    - 정확도는 100% 일 것이다.

    - overfitting 되었을 확률도 ^^..

- tree 모델의 복잡도는 노드의 개수에 비례한다.

    - tree 노드 개수에 제한이 없다면 어느 정확도에도 맞출 수 있을 것이다.

    - 따라서, tree가 자람에 따라 overfit 되는 경향이 있다.

- fitting graph for tree induction

    - ex) tree가 모집단의 특징이 아니라 훈련 데이터의 디테일한 부분을 고려하기 시작했을 때..

    - holdout data의 정확도가 떨어지는 순간 (= overfit이 시작되는 순간) 을 "sweet spot" 이라고 한다.

    - 그러므로 위의 경우 노드가 100개 정도 되는 순간부터 overfitting이 된다고 볼 수 있다.

    - 따라서 우리는 tree의 크기를 이 사이즈 (100) 로 제한해야 한다.

    - 하지만, 이론적으로 sweet spot을 정확하게 찾을 방법은 없다.

    - 따라서 이 부분은 데이터 과학자의 경험에 의해 결정해야 한다.

5. overfitting in mathematical functions

- 수학적 함수를 복잡하게 만드는 한 가지 방법은 변수나 항의 수를 늘리는 것이다.

- 더 많은 속성들을 사용하면서 모델은 훈련 데이터에 더 적합해질 수 있다. ( + overfitting 위험성)

- 즉, 변수나 항을 늘릴수록 훈련 데이터셋에서의 정확도는 증가한다.

- overfitting을 피하기 위해서는 오직 정보를 얻을 수 있는 유용한 속성들만 사용하고, 

- holdout technique을 활용해서 overfitting을 확인할 수 있다.

6. Holdout Evaluation

- 모델을 만들 때 holdout data를 빼놓고 형성한다.

- holdout data를 가지고 모델의 정확도를 평가한다.

- 목표는 모델의 일반화 성능을 추정하는것이다. 

- 답을 알고 있고, 훈련할 때 사용하지 않았기 때문에 정확도를 평가할 수 있다.

- 문제 

    - 이 테스트로부터 얻은 성능의 추정값은 단지 한번의 테스트를 통한 추정값이다.

    - 한 번의 추정만으로 모델 정확도에 확신을 얻는 방법은 운이 좋게 테스트 데이터를 한번에 잘 고르는 방법이 있겠다.

7. Cross-Validation (CV)

- holdout evaluation 의 더욱 정교화된 방법이다.

- holdout 평가를 여러번 진행한 뒤 그것의 통계값을 이용하는 방법이다.

- 추정된 성능에 대해 몇가지 통계값을 얻을 수 있다.

    - mean 평균 : 평균적으로 어느 정도의 성능이 예상되는가

    - variance 분산 : 데이터셋마다 성능이 얼마나 다른가

- k-fold cross-validation : 데이터셋을 k번으로 나누어서 나눈만큼 평가를 반복하는 방법이다.

- (ex) predict which customers are going to churn

    1) information gain

    2) classification tree

    3) 언제 tree building을 멈추는가?

        - 그렇게 복잡해지기 전에 멈춰야 한다.

        - 이 문제는 model generality와 overfittingr과 밀접한 관련이 있다.

    4) tree를 원래 데이터셋에 적용했을 때 정확도가 73%이다.

        - 이 값을 믿을 수 있는가?  다른 데이터셋에 적용해도 73%가 나올까?

        - 정확도가 73%인 것이 이 모델이 좋다는 의미인가? 좋지 않다는 의미인가?

8. Learning Curves

- 일반적으로, 모델의 일반화 성능은 어떠한 지점까지는 훈련 데이터 수를 증가시킴으로써 가능하다.

- learning curve : tree와 logistic regression에서 훈련 데이터 크기에 따른 일반화 성능을 나타낸 그래프이다.

- observations

    - decision tree가 logistic regression에 비해 더 유연하다.

    - 크기가 작은 데이터셋에 대해서는 logistic regression이 더 낫다. 

    - 크기가 큰 데이터셋에 대해서는 tree가 더 nonlienar 관계를 잘 표현한다.

- learning curve vs. fitting graphs

    - learning curve : 훈련 데이터의 일반화 성능을 보여준다. (x축 : training data 양)

    - fitting graph : 훈련 데이터 성능과 holdout 데이터 성능 2가지 모두 보여준다.  

9. Overfitting Avoidance and Complexity Control

- Regularization : 가장 대표적인 overfitting avoid 방법, 모델의 복잡도를 줄이는 방법이다.

9-1. for tree induction

- main problem

    - leaf node들이 순수해질 때까지 tree를 키우는 것

    - 이로 인해 크고 복잡한 데이터가 데이터에 맞지 않을 수 있다.

- 3 regularization

    - 더 복잡해지기 전에 멈추기

    - 충분히 tree 크기가 커질 때가지 키운 다음에, '가지치기' 해나가면서 다시 사이즈 줄이기

    - 서로 다른 크기를 가진 tree를 여러 개 만든 다음, 최선의 모델 선택하기

1) limit tree size

- 분할된 leaf node에 들어갈 개체의 최소 개수를 정해둔다. 

- 즉, 최소 개수 이하의 수가 되면 더이상 분할하지 않는다.

- 이 경우, 최소 개수를 20개로 정했기 때문에 각 그룹의 개체 수가 20개 이하가 되었을 때 growing을 멈췄다.

2) Prune An Overly Large Tree

- node와 branch들을 잘라내고, 그자리를 leaf node로 바꾸는 방법이다.

- 대체했을 때 정확도가 낮아지지 않을 때까지 진행한다.

- 성능이 떨어지지 않을 때까지 하위 그룹에서 반복되며 진행될 수 있다.

3) Build Many Trees And Pick The Best

- tree를 많이 만들어놓고, 그 중 가장 정확도가 높은 tree를 택하는 방법이다. 

9-2. for linear models

- 항이 많을수록 복잡하다.

1) Sequential forward selection (SFS)

- 순차적으로 항을 한 개씩 골라서 성능을 테스트한다. 그 중 가장 정확도가 높은 xᵢ를 선택하여 f(x) 에 넣는다.

- 그 다음, 처음으로 추가한 항을 포함하여 또 한 개의 항을 골라서 성능을 테스트한다. 그 중에서 가장 성능이 좋은 xᵢ를 선택하여 f(x) 에 넣는다.

- 이 과정을 계속 반복한다.

- 항을 추가하는 것이 테스트 데이터에서의 정확도를 더이상 높이지 않을 때까지 반복한다.

2) Sequential backward elimination (SBE)

- 위의 과정을 반대로 진행하는 것이다.

- 전체 f(x)에서 항을 한 개씩 선택하여 제거한 후 성능을 테스트한다.

- 제거했을 때 가장 성능이 좋은 xᵢ를 선택하여 제거한 후, 그 다음 또 항을 한 개 골라서 제거하고 성능을 테스트한다.

- 이 과정을 계속 반복한다.

- 마찬가지로 항을 제거하는 것이 더이상 정확도를 높이지 않을 때까지 반복한다.

10. Nested Cross-Validation

- 중첩된 CV

- 모델의 복잡도를 가장 크게 좌우하는 파라미터가 무엇인지 모를 때 사용한다.

- (ex) decision tree → number of nodes, linear model → number of features ···

- 즉, 복잡도 파라미터의 최적값을 찾기 위해 사용한다.

- (ex) What is the best number of nodes in a decision tree?

- 중첩된 loop 를 이용한다. (outer & inner loop)

    - outer loop :  만들어진 모델의 일반적인 성능 측정한다. (k-fold CV)

    - inner loop : best complexity parameter 찾아낸다.

    - inner loop → outer loop

- 단점 : inner loop 개수가 많을수록 실행 시간이 매우 길어진다.

 

수업 출처) 숙명여자대학교 소프트웨어학부 수업 "데이터사이언스개론", 박동철 교수님

1. Predictive Modeling

- 다른 속성들을 통해서 타겟 속성의 값의 모형을 찾는 것이다.

-  Nonparametric modeling

    - 모델 모양이 정해져 있지 않은 모델이다

    - 모델의 구조는 데이터로부터 결정된다.

    - (ex) classificaiton 'tree' - 가지의 수, 모양 등은 데이터를 통해서 알 수 있다.

- Parametric modeling 

    - 모델이 정해져 있다.

    - 모델의 구조는 데이터 분석가에 의해 지정된다.

    - (ex) linear classify - y = ax + b의 모양으로, 모양은 정해져 있으며 데이터로부터 파라미터인 a, b만 찾아낸다.

2. Nonparametric modeling 

- 분석가가 모델의 구조를 지정하지 않는다. 데이터로부터 학습된다.

3. Parametric modeling (= parameter learning)

- 특정 파라미터 값이 지정되지 않은채로 모델의 구조가 정의된다.

- (ex) Y = aX + b -> a, b : parameter

- 주어진 훈련 데이터셋을 통해서 최상의 파라미터 값을 찾는다.

- (ex) linear regression

- 모델의 형식은 배경 지식이나 다른 데이터 마이닝 기술들을 통해서 결정한다.

- 목적은 모델 파라미터의 '최적'값을 찾아내는 것이다.

- 이때 어떤 모델이 가장 데이터를 잘 표현하는지 결정하는 것이 중요하다.

3-1. Classification Trees

- space는 결정 범위에 의해 여러 개의 클래스로 나눠진다.

- 새로운 개체가 들어왔을 때, 개체의 타겟 값은 분류된 타겟 값을 통해 결정된다.

- 다른 방식으로도 공간을 분류할 수 있다.

3-2. Linear classifier

- linear combination을 이용해서 속성을 분류한 것이다.

- linear combination은 속성 값에 가중치를 부여하여 더한 것이다. 

- (ex) 1 x Age = Balance x -1.5 + 60

- 선을 기준으로 윗 부분 :  Age > balance x -1.5 + 60, 아랫 부분 : Age < Balance x -1.5 + 60

3-3. classification tree vs. linear classifier

- 목표는 같다. : 타겟 속성에 대해 값을 기준으로 데이터를 분류하기 위한 모델이다.

- 차이점 : 구조

- classificaiton tree

    - 각 속성 별로 class를 분류해서 값을 집어넣는 방식이다.

- linear classifier

    - 여러 속성들을 가중치를 파라미터로 하여 더해서 관계성을 찾는 방식이다.

4. Linear Classifier

- general linear classifier 

    - f(x) = w₀ + w₁x₁ + ··· + wₙxₙ

- shpe of decision boundary

    - n = 2 → line

    - n = 3 → plane

    - n = 4 → hyperplane

- goal

    - 훈련 데이터를 통해서 가장 적절한 가중치 값을 찾는 것이다. 

    - 훈련 데이터를 잘 분류하고, 새로운 데이터도 가능한 적절하게 예측할 수 있도록

    - 가중치 w𝑖 가 클수록 x𝑖가 타겟을 분류하는 데 중요한 역할을 한다는 것이다. 

    - w𝑖가 0에 가까우면 x𝑖는 보통 무시되어도 괜찮다.

- 가중치 선택하는 일반적인 방법

    - 목표에 맞는 objective function을 정의한다.

    - objective function을 극대화 (최소화) 하는 최적의 가중치 값을 찾는다.

- 다음 모델들은 같은 linear 구조이지만, 다른 objective function을 사용한다. 

    - support vector machine (SVM) : classification

    - linear regression : regression

    - logistic regression : classification

    - 동일한 linear classifier f(x) = w₀ + w₁x₁ + ··· + wₙxₙ 를 사용한다.

    - (ex) svm vs. logistic regression : 둘 다 분류 모델이지만, 다른 경계를 형성한다. 

4-1. Support Vector Machine

- linear calssifier 모델이다. 

- 속성들의 선형 조합에 기반하여 개체를 분류한다.

- "margin을 최대화하는 선이 최적의 linear classifier이다"

    - margin : 각 그룹의 값들 중 가장 바깥 쪽에 있는 값을 그은 두 dash line 사이의 거리

    - margin이 가장 큰 두 선의 중간에 있는 선이 svm의 linear classifier이다.

    - 즉, 최적의 선은 두 클래스에서 모두 멀리 떨어진 선이다.

- misclassificaiton

    - 물론 아래와 같이 한 줄로 데이터들을 완벽하게 분리할 수 없는 경우도 많다. 

- original function : margine size 최대로 하는 선

- new objective function : 잘못 분류된 훈련 데이터 개체에 패널티를 부여하는 것이다.

- 패널티는 margin 경계로부터의 거리에 비례해서 부여된다.

- 이러한 방식을 'hinge loss function' 이라고 한다.

4-2. Linear Regression

- 데이터를 가장 잘 표현하는 linear 함수를 찾는 모델이다.

- 타겟 속성의 값을 "예측" 할 때 사용된다.

- 다른 objective function을 사용하는 많은 선형 회귀 방법들이 있다.

- 일반적인 절차

    - 훈련 데이터에서 각 점들에 대한 오차를 계산한다. 

    - 오차 : 선과 점 사이의 거리

    - 오차의 절댓값들을 더한다.

    - 오차의 절대합을 최소화하는 가중치를 구한다.

4-2-1. 최소제곱법

- 가장 일반적인 표준 선형 회귀 절차이다.

- objective function : 오차의 제곱합을 최소로 하는 가중치 w₀, w₁, ··· , wₙ 찾기

- 오차의 절댓값을 더하면 선을 다르게 해도 차이가 그리 크지 않고, 수학적 계산도 어렵기 때문에 제곱합을 사용한다.

- 장점

    - 더 높은 검정력으로 지수가 높아질수록 이상치의 오차가 극대화될 것이다.

    - 이차 함수는 수학적으로 다루기 쉽다. 미분해서 도함수가 0이 되는 값이 최소값이 된다.

- 단점

    - 이상치가 선을 결정하는 데 너무 큰 영향을 미친다.

4-3. Logistic Regression 

- linear regression 과 비슷하다. 

    - 둘 다 지도학습 알고리즘이다.

    - 둘 다 라벨링된 데이터셋을 예측하기 위한 알고리즘이다. (class 값이 정해진)

    - 하지만, linear regression은 회귀 모델이고, logistic regression은 이름은 regression이지만 분류 모델이다.

- 타겟이 될 "이항" 결과 (범주형 종속 변수) 와 서로 종속되어 있는 많은 속성들이 있을 때 사용한다.

- Y = aX + bZ 일 때, Y 가 타겟이고, X와 Z가 독립인 다른 속성들이다. a와 b가 파라미터이다. 

- Y는 X와 Z의 영향을 받는다.

- 실생활의 이항 결과들은 이러한 것들이 있다.

- game (win / loss), sales( buying / not buying), loan( default / non default ), marketing( response / no response )

- 새로운 개체가 관심있는 클래스에 속할 확률을 추정할 때 linear model f(x)을 이용한다.

- (ex) f(x) = 0.85 → x가 그 특정 클래스에 속할 확률이 85%이다.

- 하지만! 이 f(x) 함수를 logistic regression에 바로 적용할 수 없다.

- f(x) 는 범위가 (-∞, ∞) 지만, logistic regression 의 범위는 확률로 [-1, 1] 이어야 하기 때문이다.

그래서 오른쪽과 같이 S-Curve 형태가 나오도록 함수를 조절하여 사용한다.

4-3-1. logistic function p(x)

- 다음 방정식을 따르는 s-shaped curve (sigmoid curve) 형태의 p(x) 함수를 적용한다.

- 확률값을 추정하여 return 한다.

- linear function f(x) 를 변형한 형태로, linear 함수를 사용하는 것은 맞다.

- ln(p/(1-p)) = w₀ + w₁x₁ + ··· + wₙxₙ = f(x)

- Odds 승산

    - 사건이 발생하지 않을 확률에 대한 사건이 발생할 확률이다.

    - p / (1-p)

    - (ex) probability = 0.5 → odds = 1, p = 0.9 → odds = 9

- log odds → ln(p / (1-p)) = f(x)

4-3-2. objective function

- likelihood model 최대화

- Σ g(x, w) 값을 최대화 하는 w𝑖 를 구하는 것이다.

- g(x, w)는 x의 특징에 기반한 x의 실제 클래스를 통해 모델의 추정 확률을 반환한다.

- 이제 라벨링된 데이터셋의 모든 개체들에 대한 g(x, w) 값을 모두 더한다.

- 그리고 다른 파라미터를 가진 모델에 대해서 또 진행한다.

- 그러면 logistic regression에 대한 다양한 가중치 집합이 생성된다.

- 가장 합이 큰 모델이 데이터에 대해 가장 높은 확률을 갖는 모델이다. (가장 가능성이 큰 모델)

- 가능성이 가장 큰 모델은 평균적으로 가능한 예제들에 대해 가장 높은 확률을 반환하고, 적절하지 않은 모델에 대해서 가장 낮은 확률을 반환한다.

- 적용

    - 위와 같이 p(x) 확률값에 따라 개체들을 분류할 수 있다.

4-4. Linear regression vs. Logistic regression

4-5. Classification trees vs. Linear classifiers

4-6. 어떤 모델이 더 좋은가..?

-  어떤 결정 경계가 가장 좋은 선택일지 아마 미리 볼 수 없을 것이다.

- 하지만 이해력의 차이가 있다.

    - logistic regression은 통계학을 잘 모르는 사람드은 이해하기 쉽지 않다.

    - decision tree는 대부분의 사람들이 이해하기 쉽다.

- 많은 경우 이해관계자들에게 모델을 만족시켜야 한다.

- 그렇기 때문에 성능과 이해도를 잘 조절하여 모델을 선택해야 한다.

5. Linear Regression 예제

- Wisconsin Breast Cancer Dataset : 유방암 진단 데이터

- 각 예는 세포 핵 이미지를 나타낸다. 

- 376개의 양성 데이터와 212개의 음성 데이터가 있다.

- attributes : 세포핵의 특성을 묘사한 디지털화된 이미지를 계산한다. 

    - radius, texture, perimeter, area 등의 각각의 속성에 대해서 평균, 표준편차, 최대값을 계산한다.

- linear equation

- test 결과 정확도가 98.8%이다. (6 mistakes / 588 images)

- 같은 데이터셋으로 classification tree 모델을 만들면 정확도가 99.1% 이다.

- Q1 : 정확도가 98.8%이면 좋은 결과인가 아닌가?

    - 그정도 값은 데이터 마이닝에서 많이 볼 수 있는 정확도 수치이다.

    - 그러나 실생활 문제에 대한 분류 모델 평가는 보다 복잡하고 어렵다.

- Q2 : classificaiton tree가 정확도가 더 높으니까 좋은 모델인가?

    - 차이는 오직 하나의 추가적인 오차로부터 발생했다.

    - 게다가, 평가된 정확도는 훈련 데이터셋으로 활용한 동일한 데이터로 평가한 것이기 때문에 높은 것이 당연하다.

6. Linear Classifier for Ranking Instances

- 많은 경우 단순히 개체가 클래스에 속하는지 아닌지만 예측하고 싶지 않을 수 있다.

- 한 클래스나 다른 클래스에 속할 가능성으로 순위를 매길 수있다.

- (ex) will the customer respond to this ad? → Which customers are mostly likely to respond to this ad?

- 이 질문을 linear classifier 을 활용해서 해결할 수 있다.

- 결정 경계로부터 가까우면 해당 클래스에 명확히 속하지 않는 개체이다. ( |f(x)| ≈ 0 )

- 결정 경계로부터 멀리 떨어질수록 해당 클래스에 속할 확률이 크다. ( |f(x)| >> 0 )

- 따라서 결정 경계로부터 멀리 떨어진 개체일수록 rank를 높게 매긴다. 

7. Nonlinear model

- 머신러닝의 경우 대부분의 모델이 nonlinear한 형태로 나타난다.

- f(x) = w₀ + w₁x₁ + ··· + wᵢxᵢ² + wⱼxⱼ³ + wₖxᵢxⱼ + ···

- nonlinear term : 곱, 나눗셈, 지수, 로그 등이 포함되어 선형으로 나타나지 않는다.

- support vector machine과 logistic regression 의 nonlinear model이다.

- Artificial neural network 인공 신경망

    - 복잡한 nonlinear function을 학습시킬 때 사용한다.

    - 많은 nonlinear function을 연결한다.

- nonlinear model로 flexibility를 너무 높이면, 그 모델은 훈련 데이터에 너무 적합하게 형성된다. → overfitting

- overfitting → 훈련 데이터에만 fit하고, 정작 예측해야 할 새로운 데이터에 적용하면 성능이 급격히 낮아진다.

- 따라서 우리는 훈련 데이터를 넘어서 새로운 데이터에도 잘 작동할 모델을 형성해야 한다.

수업 출처) 숙명여자대학교 소프트웨어학부 수업 "데이터사이언스개론", 박동철 교수님

1. Predictive Modeling 예측 모델

- 일반적인 절차

    - training data를 가장 잘 표현하는 모델 설정

    - 새로운 데이터에 모델 적용하여 결과 예측

- 아마 처음으로 classification을 생각할 것이다.

    - 새로운 데이터가 어느 클래스에 속할지 training dataset을 기반으로 확인한다.

    - (ex) 이 고객이 회사를 금방 떠날 것 같은가? → YES / NO

2. Model

- 현실을 목적에 맞는 것만 남도록 간략하게 표현한 것이다. 

- 중요한 것과 중요하지 않은 것을 기반으로 간략화한다.

- 부적절한 정보는 날리고 관련이 있는 데이터들만 남긴다.

- (ex) 지도, 청사진 

2-1. Predictive Model

- 타겟에 대해 모르는 값을 추정하는 공식이다. 

- 예측의 정확도로 성능을 평가한다.

- 수학적인 표현(ex: linear regression)과 논리적인 표현(ex: decision tree)이 있다.

2-2. Descriptive Model

- 데이터에 내재되어 있는 인사이트를 얻는 것이 주 목적인 모델이다. 

- 즉, 예측"값"을 얻는 것이 목적이 아니다.

- 예시로는 clustering, profiling 등이 있다.

- 도출된 지능과 이해가능성으로 성능을 평가한다.

- 많은 모델들이 두가지 목적을 모두 제공할 수 있다. 

3. Model Induction 모델 유도

- 데이터로부터 모델 유도

    - 특정한 사례를 일반적인 규칙으로 일반화하는 것이다.

- 모델은 통계학적 의미에서 일반적인 규칙이다.

    - 항상 100% 맞진 않는다.

- Induction algorithm 유도 알고리즘 (leaner) : 데이터로부터 모델을 형성하기 위한 절차이다. 

- Training data 훈련 데이터 (labeled data) : 모델을 유도하기 위해 유도 알고리즘에 대입하는 데이터이다. 이미 라벨 값을 알고있다.

4. Supervised Segmentation 지도 분할

4-1. Basic idea

- 타겟에 대해 서로 다른 값들을 갖는 하위 그룹으로 분할하는 방법이다.

- 즉, 그룹끼리는 타겟에 대해 같은 (비슷한) value를 가진다.

- 분할에 사용된 변수 (값, attribute) 를 예측의 타겟 속성으로 사용할 수 있다.

 - 데이터를 가장 잘 분류할 수 있는 속성을 선택하는 것이 중요하다.

4-2. Selecting Information Attributes

- 효과적으로 데이터를 분류하기 위해서는 유용한 속성을 사용해야 한다.

- 유용한 속성은 해당 변수에 대해 중요한 값을 갖는 속성이다.

- 즉, 타겟의 값을 예측하는 것을 도와줄 수 있는 속성이다.

- (Ex)

- 사람들을 'yes' 와 'no'로 분류하고자 한다.

- 속성

    - 머리 : 정사각형 / 원

    - 몸 : 직사각형 / 타원

    - 몸 색 : 검정 / 하양

- target variable : 체납 여부 - yes / no

- 어떤 속성이 사람들을 yes와 no로 가장 잘 분류할 수 있을까?

- 우리는 그룹을 가능한 pure하게 분류하고자 한다.

- pure 

    - 그룹이 타겟 값에 대해 동일한 값을 갖는 상태를 말한다.  

    - 하나의 멤버라도 다른 값을 가지면 그 그룹은 impure하다고 말한다.

- 문제

    - 속성이 완벽하게 그룹으로 분리되는 경우는 거의 없다. 

        - 머리 모양과 몸 색을 각각 그룹을 분리한 결과이다. 어떤 속성이 더 그룹을 잘 분리한 것일까?

    - 모든 속성이 위의 예제처럼 2가지로 나누어지는것은 아니다. 더 많은 경우에는 어떻게 분리할 수 있을까?

    - (연속적인) 숫자 값을 가지는 속성은 어떻게 분류하는 것이 좋을까? (ex: 나이)

- 분류 기준

    - 속성이 데이터를 얼마나 잘 분류하는지를 평가하는 공식을 만들 수 있다.

    - 그 공식은 '순도'에 기반할 수 있다. 

- Information Gain

    - 가장 대표적인 분류 기준이다.

    - 순도를 측정하는 "엔트로피"에 기반한다.

- Entropy 무질서도

    - 무질서도를 측정하는 기준이다. 타겟의 관점에서 분류가 얼마나 impure하게 되었는지 측정한다.

    - H(S) = Σ p𝑖 log₂ (1/p𝑖)

        - p𝑖 : S에서 𝑖를 가질 확률 (Σ p𝑖 = 1)

    - (Ex) 

    - attribute S = {yes, yes, yes, no, no} → p₁(yes) = 3/5, p₂(yes) = 2.5

    - H(S) = 3/5 log₂(5/3) + 2/5 log₂(5/2) = 0.97 → very impure

4-3. Information Gain

- 엔트로피는 각각의 분할이 얼마나 impure한지만 측정한다.

- 즉, 한 개의 속성만 고려한다.

- information gain은 속성이 만드는 전체 분할에 대한 엔트로피 증감 정도를 측정한다.

    - 엔트로피가 감소하면 유용한 정보이고, 엔트로피가 증가하면 정보를 얻을 수 없는 속성으로 분할한 것이다.

- IG = H(parent) - [ Σ p(c𝑖) ·H(c𝑖) ]

    - 각 child (분류된 그룹)에 대한 엔트로피는 각각의 그룹에 속하는 인스턴스의 비율에 가중된다.

- Information Gain 값이 클수록 유용한 속성이다. 

4-4. Numerical Variables

- 회귀 문제와 같이 속성 값이 "숫자형"인 경우는 카테코리값을 가진 속성보다 분류하기 어렵다.

1) Discretize 이산화

    - 한 개 이상의 분할점을 선택해서 숫자 값을 이산화하는 방법이다.

    - 그 후 카테고리형 속성과 같이 다룰 수 있다. 

2) 여러 개의 후보 분할점을 고르는 방법

    - 각각의 후보 분할점에 대해 IG 를 계산한 후 가장 IG 값이 큰 경우를 선택하는 방법이다. 

5. Classificaiton Tree Segmentation

-  여러 개의 속성을 사용해서 데이터를 분류하는 방법이다. → 트리 모양

- structure

    - interior node : 분류의 기준이 되는 속성 이름이다.

    - leaf node : 분류된 class(결과?)를 말한다.

    - branch : 속성의 구분되는 값을 말한다. (분류 기준, 범위)

    - path from the root to a leaf : 분류의 특징을 설명하는 길이다.

- procedure

    - 분류 값을 모르는 예시들이 있다.

    - root node에서부터 예시들의 특정 속성 값들로 branches를 선택하면서 interior nodes를 타고 내려온다.

    - terminal node (leaf node)에 도달하면 그것은 분류가 된 것이다.

- (ex)

    - balance = 115K, employed = no, age = 40 인 사람을 분류해보자.

    - root node인 employed 부터 no, ≥50K, <45 path를 따라서 내려온다.

    - 결과적으로 class = Not Write-off 로 특정된 leaf node에 도착한다.

    - 따라서 우리는 그 사람이 체납하지 않을 것이라고 예측할 수 있다.

- divide-and-conquer approach 

    - 전체 데이터셋을 나누기 가장 좋은 속성을 찾는다.

    - 각 서브 그룹에 대해서 재귀적으로 가장 좋은 속성들을 찾아나간다. 

- (ex) 위의 사람모형 예시

    - 일련의 과정에서 IG 값의 크기에 따라 큰 순서대로 몸 모양 - 몸 색 - 머리 모양 순으로 그룹을 분류한다.

그 결과 위와 같은 classification tree를 얻을 수 있다.

- 요약해보면, 데이터를 재귀적으로 나누는 과정이다.

- 각 과정에서 모든 속성을 테스트하고 그룹을 가장 순수하게 나누는 (IG값이 큰) 속성을 선택한다.

- 멈추는 단계는 모든 leaf node가 pure할 때, 변수를 끝까지 나눴을 때 등이 있지만, 이렇게까지 나누면 모델이 overfitting될 것이다. 

6. Visualizing Segmentation

- classification tree 결과를 공간 상에 시각화할 때 사용한다.

- 하지만, 시각화는 두세개의 특징으로만 가능하다.

- 그럼에도 고차원 공간까지 적용할 수 있는 인사이트를 얻을 수 있다.

7. 규칙

- classification tree는 구현하기 쉽기 때문에 자주 사용되며, 수학적 공식이 그렇게 복잡하지 않다. 

- 논리적 문장으로 classification tree를 구현할 수 있다.

    - 각각의 path가 statement가 된다.

    - 각 sement는 path와 "AND"로 구성된다.

8. 확률 추정

- 단순한 분류보다 확률 추정을 할 때

- (ex) he will not write-off → the probability of him writing-off = 40%

- ranking과 같이 더욱 정교한 의사결정을 해야할 때 사용할 수 있다.

- Frequency-based propbability estimation

    - 확률을 추정하기 위해 각 leaf 에서의 개체 수를 사용한다.

    - leaf에서 그에 해당하는 개체 (positive) 가 n개, 해당하지 않는 개체 (negative) 가 m개라면, 새로운 개체가 그에 해당할 확률은 n/(n+m)이 된다.

8-1. overfitting problem

- 개체 수가 아주 적은 분류 그룹의 확률은 굉장히 높아질 수 있다. 

    - (ex) 개체 수가 1개인 그룹은 무조건 100%가 나올텐데, 그것이 좋은 분류라고 할 수 있을까? - 다른 그룹의 개체 수가 나머지 99개인 경우?

8-2. Laplace correction 라플라스 보정

- 단순히 빈도를 계산하는 대신, 빈도수 기반 추정치의 smoothed된 버전을 사용하는 것이다.

- (ex) p₁ : 2 postitive, no negative, p₂ : 20 positive, no negative

    - frequency-base : p₁ = p₂ = 1

    - laplace correction : p₁ = 0.75, p₂ ≈ 0.95

- 개체 수가 증가할수록 라플라스 방정식은 빈도수 기반 측정값에 수렴한다.